The Physical Pendulum

Next: Simple Pendulum: Up: SIMPLE HARMONIC MOTION - Previous: General Properties

The Physical Pendulum

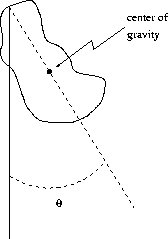
**Figure 9:** The Physical Pendulum
$\begin{figure} \begin{center} \leavevmode \epsfxsize=4 cm \epsfbox{figs/sho2.eps} \end{center}\end{figure}$

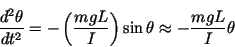$\begin{displaymath}\frac{d^2\theta }{dt^2} = - \left(\frac{mgL}{I} \right)\sin\theta\approx -\frac{mgL}{I}\theta \end{displaymath}$

(21)

where I is the moment of inertia of the pendulum, and the last expression is approximately true for small angular displacements 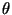$\theta$ (rads) << 1

Simple Pendulum:
Metre Stick:

gabor@theory.uwinnipeg.ca
2001-01-05