General Properties

Defining relation:

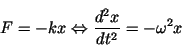$$F = -kx\Leftrightarrow\frac{d^2x}{dt^2} = -\omega^2x$$ (11)

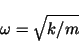$$\omega = \sqrt{k/m}$$ (12)

Solution:

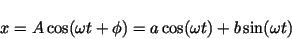$$x = A\cos(\omega t + \phi )=a\cos(\omega t)+b\sin(\omega t)$$ (13)

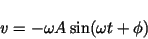$$v = -\omega A\sin(\omega t + \phi )$$ (14)

Amplitude:

| x_max| = A (15)

Period:

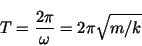$$T = \frac{2\pi }{\omega } = 2\pi\sqrt{m/k}$$ (16)

Maximum Speed:

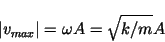$$\vert v_{max}\vert = \omega A = \sqrt{k/m}A$$ (17)

Mechanical energy:

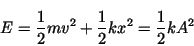$$E = \frac{1}{2}mv^2+\frac{1}{2}kx^2 = \frac{1}{2}kA^2$$ (18)

Initial Conditions:
The amplitude and phase can be determined from the initial position, x_a, and velocity, v_a, at any initial time t = t_a:

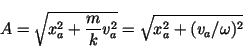$$A = \sqrt{x^2_a+\frac{m}{k}v^2_a} = \sqrt{x^2_a + (v_a/\omega )^2}$$ (19)

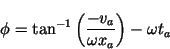$$\phi = \tan^{-1}\left(\frac{-v_a}{\omega x_a}\right)-\omega t_a$$ (20)

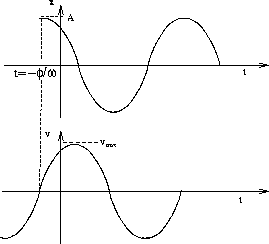
Graph of solution:

  

Figure 8: Position-time and velocity-time graphs for the SHO