



Next: The Simple Pendulum
Up: Vibrations and Waves
Previous: Elastic Potential Energy
Idea: There is a very strong analogy between circular motion and
simple
harmonic motion. Consider a particle moving with constant angular
velocity
 in a circle of radius R , as shown in Fig.13.2.
in a circle of radius R , as shown in Fig.13.2.
Figure 13.2:
Analogue Between Circular and Simple Harmonic Motion
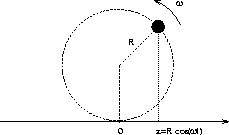 |
Its x-coordinate is given as a function of time by:
|
x = Rcos(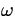 t) t)
| (9)
|
and the x-component of its tangential velocity is:
|
vx = - vtsin(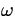 t) = - R t) = - R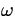 sin( sin(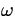 t). t).
| (10)
|
From this we deduce that
|
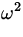 x 2 + vx2 = R 2 x 2 + vx2 = R 2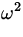
| (11)
|
which can be solved for vx :
|
vx = 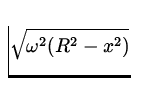 . .
| (12)
|
This is precisely the same as Eq.(13.7) relating the speed of an
SHO
to its position, providing we identify the radius with the
amplitude and
the angular velocity with 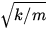 . Since the period (and
frequency) are known for circular motion (
T = 2
. Since the period (and
frequency) are known for circular motion (
T = 2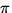 /
/ , f = 1/T ),
this analogy allows us to deduce expressions for the period (and
frequency) of
the corresponding simple harmonic oscillator:
, f = 1/T ),
this analogy allows us to deduce expressions for the period (and
frequency) of
the corresponding simple harmonic oscillator:
Similarly, the displacement and velocity as functions of time can
also be deduced:
|
x
|
=
|
Acos(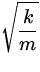 t) = Acos(2 t) = Acos(2 ft) ft)
| (14) |
|
v
|
=
|
- 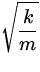 Asin( Asin(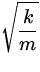 t) = - t) = - 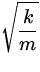 Asin(2 Asin(2 ft). ft).
| (15) |
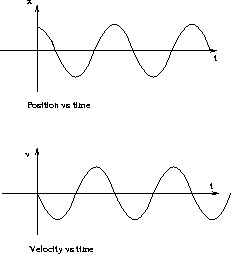
These expressions are plotted in the following figures.
Figure 13.3:
Position and Velocity as Functions of Time
 |
Note:
(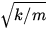 )t = 2
)t = 2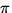 ft gives the argument of the sine and
cosine
functions in radians. Make sure that your calculator is set
to radians
when doing these problems.
ft gives the argument of the sine and
cosine
functions in radians. Make sure that your calculator is set
to radians
when doing these problems.




Next: The Simple Pendulum
Up: Vibrations and Waves
Previous: Elastic Potential Energy
www-admin@theory.uwinnipeg.ca
10/9/1997
![]()
![]()
![]()
![]()
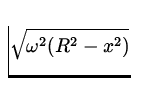 .
.
![]() )t = 2
)t = 2![]() ft gives the argument of the sine and
cosine
functions in radians. Make sure that your calculator is set
to radians
when doing these problems.
ft gives the argument of the sine and
cosine
functions in radians. Make sure that your calculator is set
to radians
when doing these problems.