Next: Comparison with Circular Motion Up: Vibrations and Waves Previous: Simple Harmonic Motion
![]()
![]()
![]()
![]()
Next: Comparison with Circular Motion
Up: Vibrations and Waves
Previous: Simple Harmonic Motion
Idea: In order to stretch a spring, it is necessary to do external work on the spring. This work is stored in the spring and is called the elastic potential energy ( PEs ). PEs depends on the spring constant, k , and the net displacement from equilibrium x and is given by:
|
PEs = | (4) |
The elastic potential energy contributes to the total mechanical
energy of the harmonic oscillator:
| E total | = | KE + PEs + PE grav | |
| = |
| (5) |
In the absence of friction, the total mechanical energy is
conserved, i.e. it is constant throughout the motion. This is
expressed
graphically (for zero gravitational potential,
PE grav = 0 )
in Fig.13.1.
Idea: When a harmonic oscillator reaches its maximum displacement, x = A , it must turn around and go back. At this turning point, the velocity is zero, and the total mechanical energy can be written in terms of the amplitude ( PEgrav = 0 ):
|
E total = | (6) |
v = 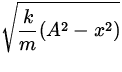 . .
| (7) |
v max = 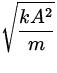 . .
| (8) |
www-admin@theory.uwinnipeg.ca