



Next: Problems
Up: Vibrations and Waves
Previous: Comparison with Circular Motion
If a pendulum of mass m attached to a string of length L is
displaced by an angle 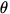 from the vertical (see figure
below),
from the vertical (see figure
below),
Figure 13.4:
The Simple Pendulum
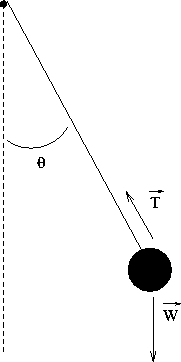 |
it experiences a net restoring force due to gravity:
|
Fr = - mgsin 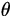 . .
| (16)
|
For small angles,
sin 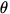
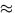
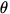 , providing
, providing 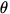 is expressed in
radians (try it on your calculator for
is expressed in
radians (try it on your calculator for
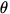 = 0.1,0.5,1.0
radians).
In terms of radians,
= 0.1,0.5,1.0
radians).
In terms of radians,
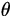 =
= 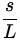 radians
radians
where s is the arc length and L is the length of the string.
Thus, for small displacements, s , the restoring force can be
written:
Fr = - 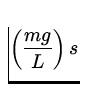 .
.
Since the restoring force is proportional to the displacement, the
pendulum is a simple harmonic oscillator with
``spring constant'' k = mg/L . The period of
a simple pendulum is therefore:
Note:
-
In this small angle approximation, the amplitude of the pendulum has no effect on the period.
This is what makes pendulums such good time keepers. As they
inevitably lose energy due to frictional forces, their amplitude
decreases, but the period remains constant.




Next: Problems
Up: Vibrations and Waves
Previous: Comparison with Circular Motion
www-admin@theory.uwinnipeg.ca
10/9/1997
![]()
![]()
![]()
![]()
![]()
![]()
![]() , providing
, providing ![]() is expressed in
radians (try it on your calculator for
is expressed in
radians (try it on your calculator for
![]() = 0.1,0.5,1.0
radians).
In terms of radians,
= 0.1,0.5,1.0
radians).
In terms of radians,
![]() =
= ![]() radians
radians
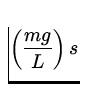 .
.