Simple Harmonic Motion

Idea: Any object that is initially displaced slightly from a stable equilibrium point will oscillate about its equilibrium position. It will, in general, experience a restoring force that depends linearly on the displacement x from equilibrium:

Hooke's Law:

F_s = - kx (1)

where the equilibrium position is chosen to have x -coordinate x = 0 and k is a constant that depends on the system under consideration. The units of k are:

$${\hbox{Newtons}\over\hbox{metre}}$$ (2)

Definitions:

• Amplitude ( A ): The maximum distance that an object moves from its equilibrium position. A simple harmonic oscillator moves back and forth between the two positions of maximum displacement, at x = A and x = - A .
• Period ( T ): The time that it takes for an oscillator to execute one complete cycle of its motion. If it starts at t = 0 at x = A , then it gets back to x = A after one full period at t = T .
• Frequency ( f ): The number of cycles (or oscillations) the object completes per unit time.

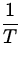  $${1\over T}$$ (3)

  The unit of frequency is usually taken to be 1 Hz = 1 cycle per second.
• Simple Harmonic Oscillator: Any object that oscillates about a stable equilibrium position and experiences a restoring force approximately described by Hooke's law. Examples of simple harmonic oscillators include: a mass attached to a spring, a molecule inside a solid, a car stuck in a ditch being ``rocked out'' and a pendulum.

Note:

• The negative sign in Hooke's law ensures that the force is always opposite to the direction of the displacement and therefore back towards the equilibrium position (i.e. a restoring force).
• The constant k in Hooke's law is traditionally called the spring constant for the system, even when the restoring force is not provided by a simple spring.
• The motion of any simple harmonic oscillator is completely characterized by two quantities: the amplitude, and the period (or frequency).