



Next: Magnetic Force on a
Up: Magnetism
Previous: The Magnetic Field
Let us consider a charge q with velocity 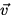 entering a region of space with a constant magnetic field
entering a region of space with a constant magnetic field 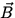 .
We assume that initially
.
We assume that initially 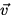 and
and 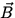 are at right angles.
The charge will experience the force of Eq.(1.2) which,
by definition, is perpendicular to the velocity
are at right angles.
The charge will experience the force of Eq.(1.2) which,
by definition, is perpendicular to the velocity 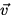 . Because
of this, the force does no work on the charge (recall
W = Fdcos
. Because
of this, the force does no work on the charge (recall
W = Fdcos 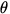 = 0
if
= 0
if
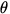 = 90 o ), and because
W =
= 90 o ), and because
W =  K =
K = 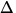 (
(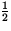 mv 2)
the speed of the charge will not change. It turns out that the charge
will move in a circular motion, with a (centripetal) acceleration
mv 2)
the speed of the charge will not change. It turns out that the charge
will move in a circular motion, with a (centripetal) acceleration
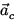 directed
toward the center of the circle, as illustrated in
Fig. 1.3.
directed
toward the center of the circle, as illustrated in
Fig. 1.3.
Figure 1.3:
Motion of a charged particle in a magnetic field
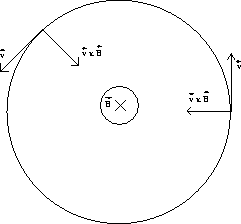 |
For such a motion we have the following relation:
This behaviour of a charged particle in a magnetic field is the principle
behind machines such as mass spectrometers, which can be used
to measure the masses of charged particles by measuring their radii
of curvature in a magnetic field.




Next: Magnetic Force on a
Up: Magnetism
Previous: The Magnetic Field
www-admin@theory.uwinnipeg.ca
10/9/1997
![]()
![]()
![]()
![]()