



Next: Motion of a Charged
Up: Magnetism
Previous: Magnetism
When we began to study electric forces we introduced the concept of
the electric field,  . In particular, we had the fundamental relation
between the force on a charge q in an electric field:
. In particular, we had the fundamental relation
between the force on a charge q in an electric field:
 = q
= q .
We will introduce a magnetic field in a similar manner.
Before doing this, however, we define what is known as
the cross product
.
We will introduce a magnetic field in a similar manner.
Before doing this, however, we define what is known as
the cross product
 x
x  between two vectors
between two vectors  and
and  . Consider two
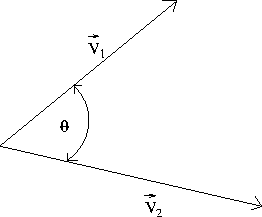
such vectors in the plane of this page with an angle
. Consider two
such vectors in the plane of this page with an angle 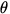 between them,
as in Fig. 1.1.
between them,
as in Fig. 1.1.
Figure 1.1:
Two vectors
 |
 x
x  , which itself
is a vector, is defined as follows:
, which itself
is a vector, is defined as follows:
As the cross product of two vectors is three dimensional
in nature, it is convenient to introduce the following notation for use
on our two dimensional paper. We represent a vector perpendicular to the
plane of this page which is directed out of the page as a circle with a
black dot in the center - this can be thought of as the tip of an arrow
coming towards you. On the other hand, a vector perpendicular to the
plane of this page which is directed into the page is represented
as a circle with a cross through the center - this can be thought of as the
tail of an arrow heading away from you. Examples of this are in
Fig. 1.2.
Figure 1.2:
Cross product of two vectors
 |
We note two general features of the cross product:
-
 x
x  =
-
=
- ![$\left[\vec {V_2}\times \vec {V_1}\right]$](img14.gif)
-
 x
x  = 0 if
= 0 if  and
and  are parallel or antiparallel, as in these cases the angle
are parallel or antiparallel, as in these cases the angle 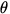 between the
two vectors is either 0 o or 180 o , for which the magnitude
of
between the
two vectors is either 0 o or 180 o , for which the magnitude
of
 x
x  given by Eq.(1.1) vanishes.
given by Eq.(1.1) vanishes.
We now consider a charge q moving at velocity 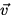 .
If this charge is in
a magnetic field
.
If this charge is in
a magnetic field 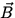 , then it experiences
a force given by
, then it experiences
a force given by
From this we see that the units of 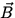 are N
are N 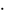 s/(m
s/(m  C), which
are given the special name Tesla (T).
We note that, analogous to the electric field,
for a given velocity
C), which
are given the special name Tesla (T).
We note that, analogous to the electric field,
for a given velocity 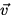 and a given magnetic field
and a given magnetic field 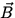 the force
on a positive charge is in the opposite direction to the force on a
negative charge.
the force
on a positive charge is in the opposite direction to the force on a
negative charge.




Next: Motion of a Charged
Up: Magnetism
Previous: Magnetism
www-admin@theory.uwinnipeg.ca
10/9/1997
![]()
![]()
![]()
![]()
![]() x
x ![]() , which itself
is a vector, is defined as follows:
, which itself
is a vector, is defined as follows:
and your fingers in the direction of
. The direction of
x
then is directed out of the palm of your hand.