



Next: Torque on a Current
Up: Magnetism
Previous: Motion of a Charged
Let us consider a long straight wire carrying a current 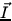 in
a magnetic field
in
a magnetic field 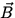 . Each charge q in the wire will experience
a force, and it is possible to find the total force on the wire by the
following arguments. Suppose there are n charges per unit volume in
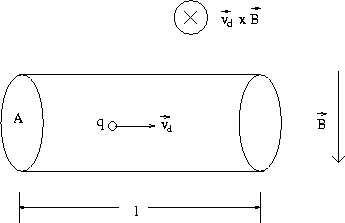
the wire of cross-sectional area A and length l , as in
Fig. 1.4.
. Each charge q in the wire will experience
a force, and it is possible to find the total force on the wire by the
following arguments. Suppose there are n charges per unit volume in
the wire of cross-sectional area A and length l , as in
Fig. 1.4.
Figure 1.4:
Current carrying wire in a magnetic field
 |
If each charge has a charge q and is moving with a drift velocity
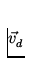 ,
then there will be a total force on the wire given by
,
then there will be a total force on the wire given by
where we recall that
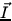 = nq
= nq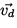 A and also that
by convention
A and also that
by convention 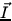 is in the direction of the flow of positive
charges.
is in the direction of the flow of positive
charges.
www-admin@theory.uwinnipeg.ca
10/9/1997
![]()
![]()
![]()
![]()
![]() ,
then there will be a total force on the wire given by
,
then there will be a total force on the wire given by