Next: About this document ... Up: Momentum and Collisions Previous: Head on Collisions and
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Momentum and Collisions
Previous: Head on Collisions and
![]()
A 0.2 kg baseball is travelling at 40 m/s. After being hit by
a bat, the ball's velocity is 50 m/s in the opposite direction. Find a) the
impulse and b) the average force exerted by the bat if the ball and bat are in
contact for 0.002 s.
Solution:
| I | = |
| | |
| = | 0.2(- 50) - 0.2(40) = - 18 kg m/s | (13) |
|
| (14) |
![]()
A 1000 kg car travelling 22 m/s (about 50 mi/hr) hits a concrete
bridge support and comes to a stop in .5 s. a) Find the average force acting
on the car and b) if the bridge support had been cushioned so that the stopping
time was increased to 3 s, what would have been the average force?
Solution:
|
| = |
| |
| = |
1000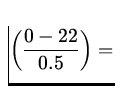 - 4.4 x 104 N - 4.4 x 104 N
| (15) |
 - 7.3 x 103 N - 7.3 x 103 N
| (16) |
![]()
A 1.0 kg object travelling at 1.0 m/s collides head on with a
2.0 kg object initially at rest. Find the velocity of each object after impact
if the collision is perfectly elastic.
Solution:
Given
m1 = 1 kg ,
m2 = 2 kg ,
v1i = 1 m/s and
v2i = 0 m/s we need to find v1f
and v2f . We use the conservation of momentum to write:
| m1v1i | = | m1v1f + m2v2f | |
| (1)(1) | = | (1)v1f + (2)v2f. |
|
| = |
| |
| (1)(12) | = | (1)v1f2 + (2)v2f2. | (17) |
| 1 | = |
v1f2 + 2![$\displaystyle\left[\frac{1-v_{1f}}{2}\right]$](img34.gif) 2 2
| |
| = |
v1f2 + 2![$\displaystyle\left[\frac{1 - 2 v_{1f} + v_{1f}^2}{4} \right]-$](img35.gif) 1 1
| ||
| = | 2v1f2 + 1 - 2v1f + v1f2 - 2 | ||
| = | 3v1f2 - 2v1f - 1 | ||
| = | (3v1f + 1)(v1f - 1). | (18) |
| v2f | = |
| |
| = |
| (19) |

Suppose the collision in the previous problem was completely
inelastic. Find a) the velocity of the objects after impact and b) the
fraction of the kinetic energy lost during the collision.
Solution:
| m1v1i | = | (m1 + m2)vf | |
| vf | = |
| (20) |
| %KElost | = |
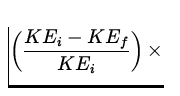 100% 100%
| |
| = |
 x 100% = 66%. x 100% = 66%.
| (21) |

In the ballistic pendulum experiment, a bullet of mass .06 kg is
fired horizontally into a wooden block of mass .2 kg. The wooden block is
suspended from the ceiling by a long string as shown in the diagram. The
collision is perfectly inelastic and after impact the bullet and the block
swing together until the block is .12 m above it's initial position. Find a)
the velocity of the bullet and block just after impact and b) the velocity of
the bullet just before impact. See Figure 6.3.
Solution:
Note: In Figure 6.3, point A is just before the bullet strikes the block, point B is just after the bullet strikes the block, and point C is when the bullet and block reach their maximum height.
We want to find vB , the velocity of the bullet and block combination just after impact, and vA , the velocity of the bullet just before impact.
| PEC | = | KEB | |
| (m1 + m2)gh | = |
| |
|
| = |
| (22) |
| m1vA + 0 | = | (m1 + m2)vB | |
|
| = |
 B = B =  .53 = 6.6 m/s. .53 = 6.6 m/s.
| (23) |
![]()
Two discs of equal mass are involved in a
perfectly elastic glancing collision. The second disc is initially at rest and
is struck by the first disc moving to the right at 5.0 m/s. After the
collision, the first disc moves in a direction that makes an angle of
37 o with its initial direction, and the second disc moves
perpendicularly to the first. Find the speed of each disc after the
collision.
Solution:
We apply the conservation of momentum in the x and y directions.
| x | : mv1i = mv1fcos 37 o + mv2fcos 53 o | ||
| y | : 0 = mv1fsin 37 o - mv2fsin 53 o |
|
5 = (cos 53 o + 1.33cos 37 o )v2f | (24) |
| v1f = 1.33v2f = 4.0 m/s. | (25) |

A car weighing 1500 kg collides with a van weighing 2500 kg at
right angles in the center of an intersection. A detective arrives at the
scene and finds that the car and van stuck together and skidded 15 m
at 53 o as shown.
After pulling out his 1301 text and doing some calculations, he charges
the owner of the car with speeding (in a 60 km/hr zone), as well as running
through a stop sign. How fast was the car going before going through the
collision? Take the coefficient of kinetic friction between the tires and the
road to be ![]() = 0.8 .
= 0.8 .
Solution:
| Ffr | = | - (mc + mv)a | |
|
| = |
- 
| |
| = |
-  = - = - | (26) |
| v 2 | = | v02 + 2ad | |
|
| = |
| (27) |
| mcvci | = | (mv + mc)vfcos 53 o | |
|
| = |
 vfcos 53 o = 14.76 m/s vfcos 53 o = 14.76 m/s
| |
| = | 53.2 km/hr | (28) |
| mvvvi | = | (mv + mc)vfsin 53 o | |
|
| = |
 vfsin 53 o = 32.7 m/s vfsin 53 o = 32.7 m/s
| |
| = | 117.6 km/hr > 60 km/hr. | (29) |
www-admin@theory.uwinnipeg.ca