Next: About this document ... Up: Electric Fields and Potentials Previous: Electric work and potential
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Electric Fields and Potentials
Previous: Electric work and potential

Three point charges, q1 = - 4 nC, q2 = 5 nC, and
q3 = 3 nC, are placed as in Fig. 1.4.
If r1 = 0.5 m and r3 = 0.8 m, find the force on q2 due to the other two charges.
Solution:
We first find the force on q2 due to q1 :
F1 = k ![]() = 9.0 x 109 x
= 9.0 x 109 x 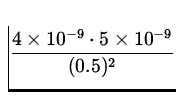 = 7.2 x 10- 7 N ,
= 7.2 x 10- 7 N ,
F3 = k ![]() = 9.0 x 109 x
= 9.0 x 109 x 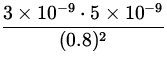 = 2.11 x 10- 7 N ,
= 2.11 x 10- 7 N ,
7.2 x 10- 7 + 2.11 x 10- 7 = 9.31 x 10- 7 N .
Thus, the total force on q2 is 9.31 x 10- 7 N directed to the left.Solution:
We resolve the contributions from q1 and q2 into
components. For q1 ,
(E1)x = k 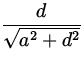 , ,
| |||
|
(E1)y = - k |
(E2)x = - k 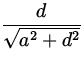 , ,
| |||
|
(E2)y = - k |
| Ex = (E1)x + (E2)x = 0, | |||
|
Ey = (E1)y + (E2)y = - 2k |
![]()
A m = 2 g ball is suspended by a l = 20 cm long string as in
Fig. 1.6 in
a constant electric field of E = 1000 N/C. If the string makes
an angle of
![]() = 15 o with respect to the vertical,
what is the net charge on the ball?
= 15 o with respect to the vertical,
what is the net charge on the ball?
Solution:
We first examine in Fig. 1.7 the forces present on the ball.
Tcos ![]() - mg = 0
- mg = 0 ![]() T =
T = ![]() ,
,
qE - Tsin ![]() = 0
= 0 ![]() q =
q = 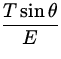 =
= 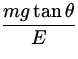 .
.
q = 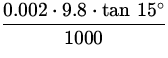 = 5.2 x 10- 6 C .
= 5.2 x 10- 6 C .
![]()
The three charges in Fig. 1.8, with q1 = 8 nC, q2 = 2 nC, and
q3 = - 4 nC, are separated by distances r2 = 3 cm and
r3 = 4 cm. How much work is required to move q1 to
infinity?
Solution:
We will first calculate the electric potential V due to
a point charge q a distance r away as
V = k ![]() ,
,
V2 = k ![]() = 9.0 x 109 x
= 9.0 x 109 x 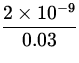 = 600 V ,
= 600 V ,
V3 = k ![]() = 9.0 x 109 x
= 9.0 x 109 x 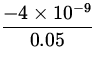 = - 720 V ,
= - 720 V ,
V = 600 + (- 720) = - 120 V ,
and so the work required to move q1 to infinity is
W = - q1![]() V = - q1 x (Vf - Vi) = - 8 x 10- 9 x
V = - q1 x (Vf - Vi) = - 8 x 10- 9 x ![]() - 9.6 x 10- 7 J .
- 9.6 x 10- 7 J .
![]()
A constant electric field E = 2000 V/m exists as in Fig. 1.9.
A 10 ![]() C charge of mass 20 g, initially at rest at x = - 1 m,
is released. What is its speed at x = 5 m?
C charge of mass 20 g, initially at rest at x = - 1 m,
is released. What is its speed at x = 5 m?
Solution:
We first find the potential difference between the two points
of interest:
E = - ![]() = -
= - 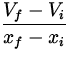
![]()
![]() V = - E
V = - E![]() x = - 2000
x = - 2000![]() - 12,000 V .
- 12,000 V .
W = - q![]() V = - 10 x 10- 6
V = - 10 x 10- 6 ![]() (- 12,000) = 0.12 J .
(- 12,000) = 0.12 J .
W = ![]() K = Kf - Ki =
K = Kf - Ki = ![]() mv 2 - 0
mv 2 - 0 ![]() v =
v = 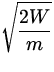 =
= 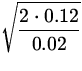 = 3.46 m / s .
= 3.46 m / s .
www-admin@theory.uwinnipeg.ca