Electric work and potential difference

The vector nature of the electric force and field makes problems involving more than a few point charges prohibitively difficult. In many instances it is possible to attack a problem using a scalar quantity called the electric potential. To introduce it, suppose we have a region of space where the electric field is constant, as in Fig. 1.2.

  

Figure 1.2: Motion of a point charge q in a constant electric field

We now place a charge q at y₁ which moves, by the electric force, to the point y₂ . The work done by the electric force is given by

 

W = Fd = qE(y₂ - y₁). (6)

We can write this relation in terms of a change in an electric potential energy PE :

 

$$\equiv \Delta$$ (7)

and also introduce the electric potential difference $\Delta$V as

 

$$\Delta \equiv \Delta$$ (8)

Comparing Eqs.(1.6,1.7,1.8), we find

 

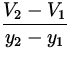$${\frac{\Delta\,V}{\Delta y}} {\frac{V_2-V_1}{y_2-y_1}}$$ (9)

From Eq.(1.7) we see that the units of electric potential energy PE are the same as those of work, which are Joules (J.). The units of potential difference $\Delta$V are found from Eq.(1.8) to be J/C, which is given the special name Volt (V). Eq.(1.9) allows us to then infer that the units of electric field E , which we earlier found to be N/C, can also be expressed as V/m.

We can from Eqs.(1.6,1.7,1.8) come up with expressions giving the electric potential energy PE and potential V at any point. Such expressions involve an arbitrary constant C :
 

$$\Rightarrow \Delta$$

$$\Rightarrow \Delta$$ (10)

The presence of the constant C stems from the fact that it is only differences in potential energy or potential which enter into the definitions of Eqs.(1.7,1.8); this is exactly analogous to the situation for gravitational potential energy, where one is free to choose the zero point at will.

Although these considerations have been for a constant electric field, the defining relation of Eq.(1.7) for the electric potential energy and that of Eq.(1.8) for the electric potential are general. Note, however, that Eq.(1.9) relating the electric field to the potential difference and the particular expressions of Eq.(1.10) for the potential energy and potential hold only for a constant electric field. If the electric field is not constant, these latter expressions change. The derivation involves some advanced mathematical techniques due to the fact that the electric force changes from point to point. We quote here the corresponding results for point charges. For this we imagine a point charge q moving from a point A to a point B in the presence of a second point charge Q , as in Fig. 1.3.

  

Figure 1.3: Motion of a point charge q in the presence of another point charge Q

We assume A is a distance r₁ from Q and B is a distance r₂ from Q . The work done by the electric force can be found using Coulomb's law (1.2), which can subsequently be related to a change in potential energy $\Delta$ PE through Eq.(1.7). The potential difference $\Delta$V can then be introduced through Eq.(1.8). One finds

$${\frac{qQ}{r}}$$ (11)

$${\frac{Q}{r}}$$

A convenient and popular choice for the constant C in this instance is C = 0 , for which V(r = $\infty$) = 0 . The nice aspect of the electric potential energy and potential is that in the presence of multiple charges one simply adds algebraically the corresponding expressions for the individual charges to find the net result.