Next: About this document ... Up: Vibrations and Waves Previous: The Simple Pendulum
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Vibrations and Waves
Previous: The Simple Pendulum

A 0.5 kg mass is hung on a vertical massless spring. The new
equilibrium position
of the spring is found to be 3 cm below the equilibrium position
of the
spring without the mass. a) What is the spring constant, k ? b)
Show that the
mass and spring system oscillates with simple harmonic motion about
the new
equilibrium position.
Solution:
|
| (18) |
|
| = |
| |
| = |
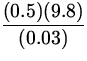 = 163 N/m . = 163 N/m .
|
Fs = k(x eq - s)
The total force upward is thereforeF tot = Fs - mg = kx eq - ks - mg
Since the equilibrium position obeys Eq.(13.18), the equation for the acceleration of the mass reduces to:| F tot = - ks | (19) |
![]()
Consider a SHO with m = 0.5 kg, k = 10 N/m and amplitude
A = 3
cm. a) What is the total energy of the oscillator? b) What is its
maximum
speed? c) What is the speed when x = 2 cm? d) What are the kinetic
and
potential energies when x = 2 cm?
Solution:
E total = ![]() kA 2 =
kA 2 = ![]() (10)(0.03) = 0.0045 J
(10)(0.03) = 0.0045 J
v max = 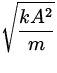 =
= 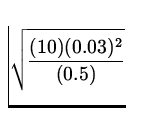 = 0.134 m/s
= 0.134 m/s
| v | = |
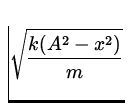
| |
| = |
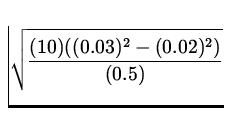 = 0.10 m/s = 0.10 m/s
|
| PEs | = |
| |
| KE | = |
|
![]()
If the oscillator in the above problem is released from rest
at x = A
when the clock is set to t = 0 seconds, a) determine the position
and
velocity of the oscillator at t = 2 s. b) At what time does the
oscillator get to x = - 1 cm?
Solution:
| x(t) | = |
Acos 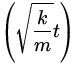
| |
| = |
(0.03)cos 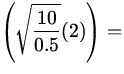 - 0.027 m - 0.027 m
|
| v(t) | = |
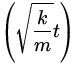
| |
| v(2) | = |
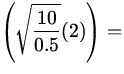 0.062 m/s 0.062 m/s
|
| x(t) | = |
Acos 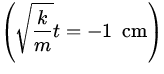
| |
|
| = |
| |
| = |
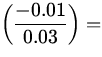 0.43 s 0.43 s
|
![]()
If the mass in the above problem experiences a constant
frictional
force of 0.1 N and is released from rest at x = A , a) what is
the velocity
of the mass when it first passes through the equilibrium position
at x = 0 . b) At what
value of x does the velocity of the mass first go to zero after
it has been
released?
Solution:
| W ext | = |
| |
| - F frd | = |
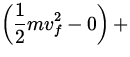 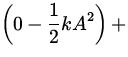 0 0
| |
|
| = |
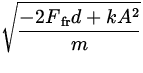
| |
| = |
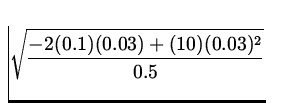 = 0.077 m/s = 0.077 m/s
|
| W ext | = |
| |
| - F frd | = |
0 + 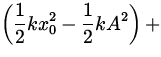 0 0
| |
| - F fr(A - x0) | = |
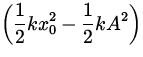
| |
|
| = | kx02 - 2F fricx0 - kA 2 + 2F fric | |
| = |
(10)x02 - 2(0.1)x0 + | ||
| = | (10)x02 - 0.2x0 - 0.003 |
| x0 | = |
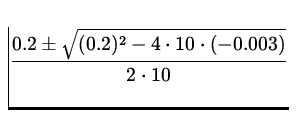 m m
| |
| = | - 0.01 m or 0.03 m | (20) |
![]()
A simple pendulum is used in a
physics laboratory experiment to obtain an experimental value for
the
gravitational acceleration, g . A student measures the length of
the
pendulum to be 0.510 meters, displaces it 10 o from the
equilibrium
position, and releases it. Using a stopwatch, the student
determines that
the period of the pendulum is 1.44 s. Determine the experimental
value of
the gravitational acceleration.
Solution:
Since the angle through which the pendulum is initially displaced
is small,
Eq.(13.17) in the Lecture Notes is valid for the period T :
| T | = |
2 | |
|
| = |
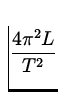
| |
| = |
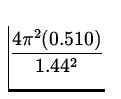 = 9.71 m/s 2 = 9.71 m/s 2
|
www-admin@theory.uwinnipeg.ca