The Uncertainty Principle

One important consequence of the wave-particle duality of nature was discovered by Heisenberg, and is called the uncertainty principle. To formulate it, let us imagine that we want to measure the position and the momentum of a particular particle. To do so we must ``see'' the particle, and so we shine some light of wavelength 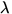$\lambda$ on it. We recall in the last chapter that there is a limit to the resolving power of the light used to see the particle given by the wavelength of light used. This gives an uncertainty in the particle's position:

 

$$\Delta \sim \lambda$$ (11)

This results from considering the light as a wave. However, viewed as a photon, the light when striking the particle could give up some or all of its momentum to the particle. Since we don't know how much it gave up, as we don't measure the photon's properties, there is an uncertainty in the momentum of the particle; using Eq.(27.8), we find

 

$$\Delta \sim {\frac{h}{\lambda}}$$ (12)

Combining Eqs.(27.11,27.12), we find

 

$$\Delta \Delta \sim$$ (13)

Note that this is independent of the wavelength used, and says there is a limit in principle as to how accurately one can simultaneously measure the position and momentum of a particle - if one tries to measure the position more accurately by using light of a shorter wavelength, then the uncertainty in momentum grows, whereas if one uses light of a longer wavelength in order to reduce the uncertainty in momentum, then the uncertainty in position grows. One cannot reduce both down to zero simultaneously - this is a direct consequence of the wave-particle duality of nature.

The arguments used in deriving Eq.(27.13) are somewhat rough. A more refined treatment, developed by Heisenberg, results in the following relation:

 

$$\Delta \Delta \ge {\frac{h}{4\pi}}$$ (14)

As with de Broglie waves, for everyday macroscopic objects such as bowling balls the uncertainty principle plays a negligible role in limiting the accuracy of measurements, as we shall see in some examples. However, for microscopic objects such as electrons in atoms the uncertainty principle does become a very important consideration.