Next: About this document ... Up: Quantum Physics Previous: The Uncertainty Principle
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Quantum Physics
Previous: The Uncertainty Principle
![]()
A quantum of electromagnetic radiation has an energy of 2.0 keV.
What is the associated wavelength?
Solution:
We will use Planck's relation
E = hf = ![]() .
.
hc = 6.63 x 10- 34 J ![]() s x 3.0 x 108
s x 3.0 x 108![]() x
x 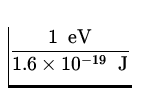 x
x 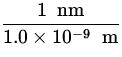 = 1243 eV
= 1243 eV ![]() nm .
nm .
![]() =
= ![]() =
= 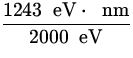 = 0.62 nm .
= 0.62 nm .
![]()
A 5 kg mass attached to a spring of spring constant k = 400 N/m is undergoing
simple harmonic motion on a flat frictionless surface with an amplitude
of 10 cm. If we assume the energy levels are quantized according to
the Planck relation E = nhf , what is the corresponding quantum number n ?
Solution:
We first find the total energy associated with the system as
E = ![]() kA 2 =
kA 2 = ![]()
![]() 400
400 ![]() (0.1)2 = 2 J .
(0.1)2 = 2 J .
f = ![]() =
= ![]()
![]() =
= ![]()
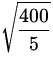 = 1.42 Hz .
= 1.42 Hz .
n = ![]() =
= 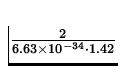 = 2.12 x 1033.
= 2.12 x 1033.
![]() E = (n + 1)hf - nhf = hf = 6.63 x 10- 34
E = (n + 1)hf - nhf = hf = 6.63 x 10- 34 ![]() 1.42 = 9.4 x 10- 34 J .
1.42 = 9.4 x 10- 34 J .
![]()
Red light of wavelength 670.0 nm produces photoelectrons from a certain metal
which requires a stopping potential of 0.5 V to stop. What is the work function
and threshold wavelength of the metal?
Solution:
We shall use the Einstein relation
eV = hf - ![]() =
= ![]() -
- ![]() .
.
![]() =
= ![]() - eV =
- eV = 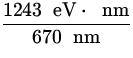 - 0.5 eV = 1.36 eV .
- 0.5 eV = 1.36 eV .
![]() =
= ![]() =
= 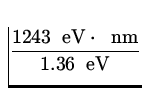 = 917.2 nm .
= 917.2 nm .
![]()
What minimum accelerating voltage would be required for an electron if
it was to give up all of its energy in a collision with a target and
produce an x-ray of wavelength 0.03 nm?
Solution:
When an electron is accelerated through a potential difference V ,
it acquires an energy eV . If this energy went into producing a photon
of energy E , with associated wavelength hc/![]() , we have
, we have
E = ![]() = eV =
= eV = 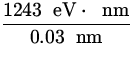 = 41,433 eV ,
= 41,433 eV ,
V = ![]() =
= 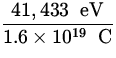 x
x 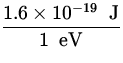 = 41,433
= 41,433![]() = 41,433 V .
= 41,433 V .
![]()
The resolving power of a microscope is approximately equal to that of the
wavelength of the light used. In an electron microscope, electrons are used
as the ``light'' source. What kinetic energy of electrons is needed if
the resolving power is required to be 10- 11 m, which would enable
one to ``see'' an atom?
Solution:
By the de Broglie hypothesis, the wavelength ![]() of a particle is
related to its momentum p by
of a particle is
related to its momentum p by
![]() =
= ![]() =
= ![]() .
.
v = ![]() =
= 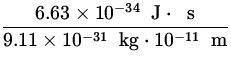 = 7.28 x 107
= 7.28 x 107![]() .
.
E = ![]() mv 2 =
mv 2 = ![]() x 9.11 x 10- 31 kg x
x 9.11 x 10- 31 kg x 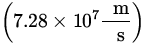 2 x
2 x 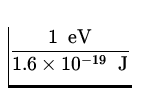 = 15.1 keV .
= 15.1 keV .
![]()
Suppose visible light of wavelength
![]() = 5 x 10- 7 m is
used to determine the position of an electron to within the wavelength
of the light. What is the minimum uncertainty in the electron's speed?
= 5 x 10- 7 m is
used to determine the position of an electron to within the wavelength
of the light. What is the minimum uncertainty in the electron's speed?
Solution:
We shall use the Heisenberg uncertainty relation
![]() x
x ![]() p =
p = ![]() .
.
![]() v =
v = 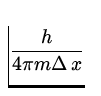 =
= 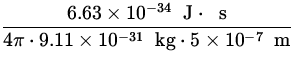 = 115.8
= 115.8![]() .
.
www-admin@theory.uwinnipeg.ca