



Next: Compton Scattering
Up: Quantum Physics
Previous: Blackbody Radiation
This situation changed in 1905 when Einstein extended
the photon picture to explain another phenomenon of
light which could
not be accounted for in the conventional
wave picture - the photoelectric effect.
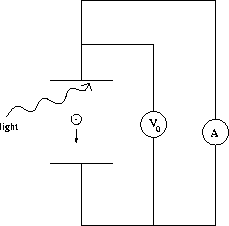
In this effect light is shone on a metal, and electrons are released.
As indicated
in Fig. 27.3,
these electrons can be attracted towards a positively
charged
plate a certain distance below, thereby establishing a photoelectric
current.
Figure 27.3:
A photoelectric effect experiment
 |
It is convenient not to measure this current itself but to measure the
stopping
potential V0 required to reduce this current to zero. The stopping
potential is related to the (maximum) kinetic energy of the ejected
electrons by
|
eV0 = KE max =  mv max2. mv max2.
| (4)
|
There were several failings of the wave picture of light when applied to
this phenomenon, but the most notable was the following:
No photoelectric electrons are emitted if the frequency of the light
falls below some cutoff frequency, fc .
This aspect of the photoelectric effect is impossible to understand within the
wave picture of light, as within that picture the energy of the light beam
which gives the electrons their energy does not depend on the frequency.
Einstein came up with an explanation of the photoelectric effect which
built upon
Planck's photon hypothesis. In this theory Einstein assumed that
photons have
an energy equal to the energy difference between
adjacent levels of a blackbody:
When these photons hit the metal, they could give up some or all of
their energy to an electron. A certain amount of energy would be
required to release the electrons from their bonds to the metal - this energy
is called the work function, 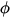 , of the metal. The remaining energy
would appear as kinetic energy of the released electron. Thus, the maximum
kinetic energy the electrons could have is
, of the metal. The remaining energy
would appear as kinetic energy of the released electron. Thus, the maximum
kinetic energy the electrons could have is
|
KE max = eV0 = hf -  = =  - -  . .
| (6)
|
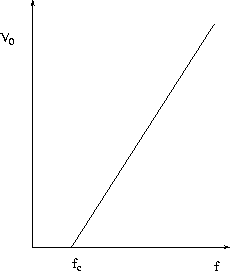
Thus, a graph such as in Fig. 27.4
of the stopping potential V0 vs. the frequency f is
a straight line, with slope related to Planck's constant h and x -intercept
being the cutoff frequency, fc where V0 = 0 :
|
fc =  = =  , ,
| (7)
|
where 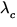 is the corresponding cutoff wavelength. This behaviour is
observed experimentally, and the success of this explanation made more and more
people take the photon picture of light seriously.
is the corresponding cutoff wavelength. This behaviour is
observed experimentally, and the success of this explanation made more and more
people take the photon picture of light seriously.
Figure 27.4:
Data from a photoelectric effect experiment
 |




Next: Compton Scattering
Up: Quantum Physics
Previous: Blackbody Radiation
www-admin@theory.uwinnipeg.ca
10/9/1997
![]()
![]()
![]()
![]()