Young's Double Slit Experiment

This is a classic example of interference effects in light waves. Two light rays pass through two slits, separated by a distance d and strike a screen a distance, L , from the slits, as in Fig. 22.10.

  

Figure 22.10: Double slit diffraction

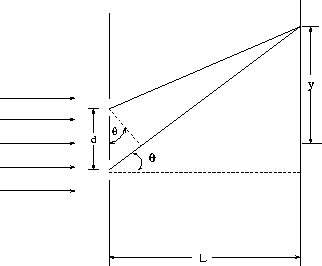If d < < L then the difference in path length r₁ - r₂ travelled by the two rays is approximately:

r₁ - r₂ $$\approx$$ dsin $$\theta$$

where $\theta$ is approximately equal to the angle that the rays make relative to a perpendicular line joining the slits to the screen.

If the rays were in phase when they passed through the slits, then the condition for constructive interference at the screen is:

dsin $$\theta$$ = m$$\lambda$$ ,m = $$\pm$$ 1, $$\pm$$ 2,...

whereas the condition for destructive interference at the screen is:

dsin $$\theta$$ = (m + $${1\over 2}$$)$$\lambda$$ ,m = $$\pm$$ 1, $$\pm$$ 2,...

The points of constructive interference will appear as bright bands on the screen and the points of destructive interference will appear as dark bands. These dark and bright spots are called interference fringes. Note:

• In the case that y , the distance from the interference fringe to the point of the screen opposite the center of the slits (see Fig.22.10) is much less than L ( y < < L ), one can use the approximate formula:

  sin $$\theta$$ $$\approx$$ y/L

  so that the formulas specifying the y - coordinates of the bright and dark spots, respectively are:

  y ^B_m = $${\frac{m\lambda L}{d}}$$ brightspots

  y ^D_m = $${\frac{(m+{1\over2})\lambda L}{d}}$$ darkspots

  The spacing between the dark spots is

  $$\Delta$$y = $${\frac{\lambda L}{d}}$$

• If d < < L then the spacing between the interference can be large even when the wavelength of the light is very small (as in the case of visible light). This give a method for (indirectly) measuring the wavelength of light. (See Ex.6 at the end of this Chapter.)
• The above formulas assume that the slit width is very small compared to the wavelength of light, so that the slits behave essentially like point sources of light.