Next: About this document ... Up: Wave Properties of Light Previous: Phase Change on Reflection
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Wave Properties of Light
Previous: Phase Change on Reflection
![]()
Two light pulses are emitted simultaneously and hit a screen
directly in front of them. If one light pulse passes through 6.2
m of ice on its way to the screen, what is the time difference
between the arrival of the two pulses at the screen? (The index of
refraction of ice is 1.309.)
Solution:
Suppose the distance to the screen is D . The time it
takes for the first pulse to arrive is:
t1 = ![]()
t2 = 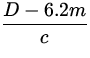 +
+ ![]()
|
| = | t2 - t1 | |
| = |
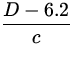 - - 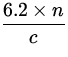
| ||
| = |
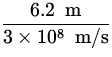 - - 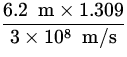
| ||
| = | 2.705 x 10- 8 s - 12.067 x 10- 8 s | ||
| = | 6.38 x 10- 9 sec | (4) |
![]()
A light ray of wavelength
![]() = 589 nm is incident on
glass with an angle of incidence of 30 o . The index of
refraction of glass is 1.52. a)What is the angle of refraction?
b) What are the speed and wavelength of the light inside the
glass?
= 589 nm is incident on
glass with an angle of incidence of 30 o . The index of
refraction of glass is 1.52. a)What is the angle of refraction?
b) What are the speed and wavelength of the light inside the
glass?
Solution:
|
sin | = |
| |
| = |
| ||
|
| = | 19.2 o | (5) |
|
| = |
| |
| = | 387 x 10- 9 m = 387 nm | ||
| v2 | = |
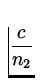 = = 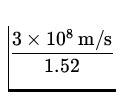 = 2 x 108 m/s = 2 x 108 m/s
| (6) |

Solution:
First calculate the angle of refraction inside the glass:
sin ![]() =
= ![]() sin
sin ![]()
|
sin | = |
| |
| = |
| ||
| = |
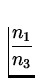 sin sin | (7) |

A fish lives at the bottom of a lake 10m deep filled with
water whose index of refraction 1.52.
a) At what angle relative to the normal must the fish look up
towards the surface of the water in order to see a fisherman who
is sitting on a distant shore?
b)What is the closest that another fish living at the bottom of
the lake can approach in order that the first fish can see it by
looking towards the surface?
Solution:
|
sin | = |
| |
|
| = | 41 o | (8) |
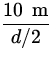 = sin
= sin ![]() =
= ![]() =
= ![]()
d = 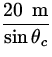 = 20 m x 1.52 x = 30 m
= 20 m x 1.52 x = 30 m
![]()
White light approaches one side of a glass prism at an angle
of incidence of 40 o as shown in the diagram below. The apex
angle of the prism is 60 o .
Solution:
First calculate the angle of refraction ![]() inside the
prism.
inside the
prism.
sin ![]() =
= ![]() sin
sin ![]()
|
sin | = |
| |
|
| = | 25.2 o | |
sin 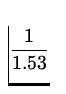 sin 40 sin 40
| |||
|
|
|
(90 o - | (9) |
|
| (10) |
![]() = 60 o - 25.2 o = 34.8 o
= 60 o - 25.2 o = 34.8 o
![]() = 60 o - 24.8 o = 35.2 o
= 60 o - 24.8 o = 35.2 o
|
sin | (11) |
|
| = |
| |
|
| = |
|
![]()
Monochromatic light goes through two thin slits 0.03mm apart.
It is found
that the second bright fringe on a screen 1.2 m away is 4.5 cm from
the center.
What is the wavelength of the light?
Solution:
Using:
y2 = n![]()
![]()
![]() =
= ![]() =
= 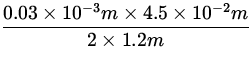 = 5.6 x 10- 7m = 560 nm
= 5.6 x 10- 7m = 560 nm
Note: This problem shows that is possible to measure very short wavelengths using the double slit experiment quite accurately as long as L/d is very large.

A radio transmitter transmits signals to a receiver 500m away
along two
paths. One is directly from the transmitter to the receiver, the
other
is bounced off a mountain a distance x directly behind the
receiver. (See Fig. (22.16))
Solution:
Since the rays bounce off a more dense mountain, there
is a phase change on reflection, so the condition for destructive
interference is:
r1 - r2 = 2x = (m + ![]() )
)![]()
x = ![]() = 75 m
= 75 m
www-admin@theory.uwinnipeg.ca