Next: About this document ... Up: Current and Resistance (Ch. Previous: Kirchhoff's Laws
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Current and Resistance (Ch.
Previous: Kirchhoff's Laws
![]()
An aluminum wire with a cross-sectional area of
4 x 10- 6 m 2 carries a current of
5 A. Find the drift speed of the electrons in the
wire, assuming each aluminum atom contributes on electron.
The density of aluminum is 2.7 g/cm 3.
Solution:
For this we will use
I = nqvdA.
To find the number of charges per unit volume, n , we find from the periodic table that the atomic mass of aluminum is 26.98 g/mol. Since 1 mol of a substance contains Avagadro's number NA = 6.02 x 1023 of particles, we find
n = 6.02 x 1023 x
x  x
x  x
x  3 = 6.02 x 1028
3 = 6.02 x 1028
vd = ![]() =
= ![]() = 1.3 x 10- 4 m / s .
= 1.3 x 10- 4 m / s .
![]()
Suppose one wants to make a 0.5 ![]() resistor
out of 1 g of Copper. If the resistor is a uniform
cylinder, what is the diameter and length required?
resistor
out of 1 g of Copper. If the resistor is a uniform
cylinder, what is the diameter and length required?
Solution:
We will relate the resistance R to the resistivity by
R = ![]()
![]() ,
,
V = 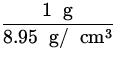 x
x  3 = 1.12 x 10- 7 m 3.
3 = 1.12 x 10- 7 m 3.
R = ![]()
![]() =
= ![]()
![]()
![]() L =
L =  = =
= = 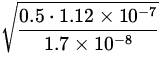 = 1.8 m .
= 1.8 m .
A = ![]() =
= ![]()
![]() d 2
d 2 ![]() d =
d = ![]() =
=  = 2.8 x 10- 4 m .
= 2.8 x 10- 4 m .
![]()
A small motor draws a current of 2 A from a 120 V line.
Assuming 100% efficiency, what is the cost of operating
the motor for 10 hours if the power company charges
$0.050/kWh?
Solution:
The motor has a power output of
P = VI = 2 x 120 = 240 W .
Operating it for 10 hours will consume an amount of energy
E = Pt = 240 W x 10 h x  = 2.4 kWh .
= 2.4 kWh .
![]()
Find the current through R4 in the circuit in Fig. 17.9
if V = 30 V,
R1 = 12 ![]() ,
R2 = 18
,
R2 = 18 ![]() ,
R3 = 9
,
R3 = 9 ![]() , and
R4 = 6
, and
R4 = 6 ![]() .
.
Solution:
We first reduce the four resistors to one equivalent resistance.
The resistors R1 , R2 , and R3 are in parallel;
they have an equivalent resistance
![]() =
= ![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]() +
+ ![]()
![]() Rp = 3
Rp = 3 ![]() .
.
R = R1 + Rp = 12 + 3 = 15 ![]() .
.
I = ![]() =
= ![]() = 2 A ,
= 2 A ,
Vp = IRp = 2 x 3 = 6 V .
This potential difference is the same across R2 , R3 , and R4 , and in particular we have through R4
I4R4 = 6 ![]() I4 =
I4 = ![]() = 1 A .
= 1 A .
![]()
Find the power lost in the 50 ![]() resistor in the
circuit in Fig. 17.10.
resistor in the
circuit in Fig. 17.10.
Solution:
We begin by labelling the unknown currents as indicated.
Applying Kirchhoff's junction rule, we find
I1 = I2 + I3.
We next use Kirchhoff's loop rule; for the top loop, going clockwise, we find
30I3 + 50I3 - 40I2 = 0 ![]() I3 =
I3 = ![]() I2,
I2,
40I2 - 20 + 10I1 = 0 ![]() I1 = 2 - 4I2.
I1 = 2 - 4I2.
2 - 4I2 = I2 + ![]() I2
I2 ![]() I2 =
I2 = ![]() A ,
A ,
|
I3 = | |||
|
I1 = 2 - 4I2 = |
As a check on our algebra, we can verify that by going around the outer loop
30I3 + 50I3 - 20 + 10I1 = 0,
as it should. We then know the current through the 50
P = I 2R =  2 x 50 = 1.65 W .
2 x 50 = 1.65 W .
![]()
Find the currents through all three resistors in the
circuit in Fig. 17.11.
Solution:
We begin by labeling the unknown currents as indicated.
Applying Kirchhoff's junction rule, we find
I1 + I3 = I2.
We next use Kirchhoff's loop rule; for the top loop, going clockwise, we find
20 - 100I2 - 20I3 = 0 ![]() I3 = 1 - 5I2,
I3 = 1 - 5I2,
100I2 - 60 + 10I1 = 0 ![]() I1 = 6 - 10I2.
I1 = 6 - 10I2.
(1 - 5I2) + (6 - 10I2) = I2 ![]() I2 =
I2 = ![]() A ,
A ,
|
I3 = 1 - 5I2 = - | |||
|
I1 = 6 - 10I2 = |
As a check on our algebra, we can verify that by going around the outer loop
- 20I3 + 20 - 60 + 10I1 = 0,
as it should. Note that for this check we must explicitly use the negative value found for I3 .www-admin@theory.uwinnipeg.ca