Kirchhoff's Laws

Although useful to be able to reduce series and parallel resistors in a circuit when they occur, circuits in general are not composed exclusively of such combinations. For such cases there are a powerful set of relations called Kirchhoff's laws which enable one to analyze arbitrary circuits. There are two such laws:

• the 1 ^st law or the junction rule: for a given junction or node in a circuit, the sum of the currents entering equals the sum of the currents leaving. This law is a statement of charge conservation. For example, in Fig. 17.6,
  
    

  Figure 17.6: Illustration of Kirchhoff's junction rule

  
  
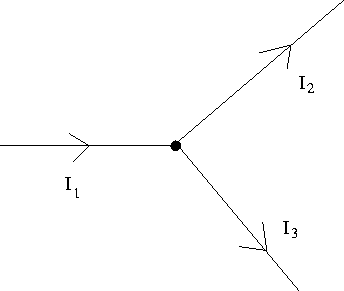  the junction rule tells us I₁ = I₂ + I₃ .
• the 2 ^nd law or the loop rule: around any closed loop in a circuit, the sum of the potential differences across all elements is zero. This law is a statement of energy conservation, in that any charge that starts and ends up at the same point with the same velocity must have gained as much energy as it lost. For example, in Fig. 17.7,
  
    

  Figure 17.7: Illustration of Kirchhoff's loop rule

  
  
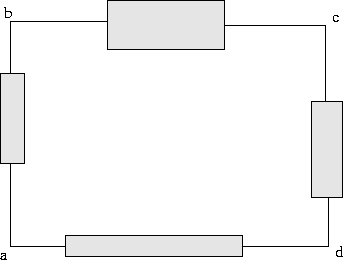  where the boxes denote a circuit element, the loop rule tells us 0 = (V_b - V_a) + (V_c - V_b) + (V_d - V_c) + (V_d - V_a) .

The second law entails certain sign conventions for potential differences across circuit elements. For batteries and resistors, these conventions are summarized in Fig. 17.8. Note that in these conventions the current always flows from a high to a low potential.

  

Figure 17.8: Sign conventions for Kirchhoff's loop rule

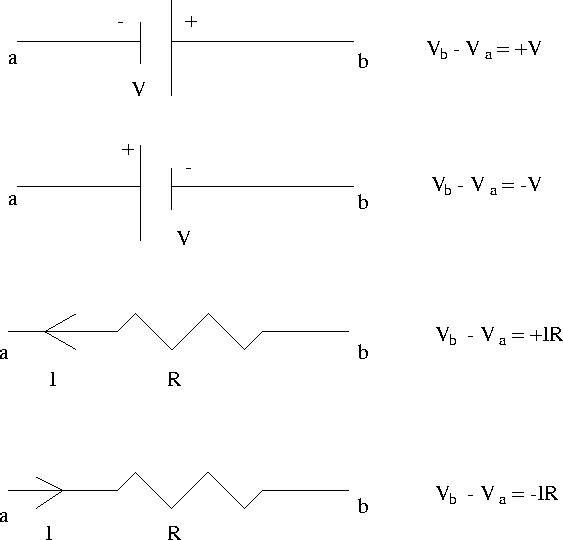In analyzing circuits using Kirchhoff's laws, it is helpful to keep in mind the following guidelines.

1.

Draw the circuit and assign labels to the known and unknown quantities, including currents in each branch. You must assign directions to currents; don't worry if you guess incorrectly the direction of a particular unknown current, as the answer resulting from the analysis in this case will simply come out negative, but with the right magnitude.

2.

Apply the junction rule to as many junctions in the circuit as possible to obtain the maximum number of independent relations.

3.

Apply the loop rule to as many loops in the circuit as necessary in order to solve for the unknowns. Note that if one has n unknowns in a circuit one will need n independent equations. In general there will be more loops present in a circuit than one needs to solve for all the unknowns; the relations resulting from these ``extra'' loops can be used as a consistency check on your final answers.

4.

Solve the resulting set of simultaneous equations for the unknown quantities.

Proficiency in analyzing circuits with Kirchhoff's laws, particularly with regard to the sign conventions and with solving simultaneous equations, comes with practice.