Gravity as Curved Space: Einstein's Theory of General Relativity

Newton's Law of Universal Gravitation had three basic flaws:

 

1.

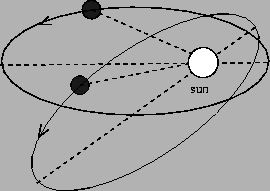
It gave the wrong prediction for the precession of the perihelion of Mercury's orbit. Mercury's orbit is elliptical, as predicted by Newton's theory of gravity, but the ellipse doesn't stay in precisely the same place all the time. It precesses, which is to say that as Mercury orbits the sun, the entire ellipse rotates about the focal point (i.e. the sun) as shown in the Figure below. This precession is very small; only 570 seconds of arc per century. A second of arc is 1/360 of a degree. Most of this precession could be understood in the context of Newton's theory of gravity by taking into account perturbations of the orbit due to the presence of other planets. However, once this was done, there still remained a discrepancy of about 40 seconds of arc per century between the prediction, and the observed value. This discrepancy was a complete mystery to scientists at the turn of the century. They even went as far as postulating the existence of an unseen planet (Vulcan) on the far side of the Sun in order to explain it. It was not until Einstein published his work on the general theory of relativity that the perihelion shift of Mercury was truly understood.

  

Figure 6.3: Precession of Mercury's orbit

2.

It did not explain why the gravitational force on an object was proportional to its inertial mass. In other words it did not explain why gravitational acceleration is independent of the mass or composition of an object.

3.

It was inconsistent with the Special Theory of Relativity. That is, if an instantaneous force of gravitational attraction exists between two objects then information about the location of one object would be transmitted to another object instantaneously by changes in the gravitational force. Thus it would be possible to send information faster than the speed of light.

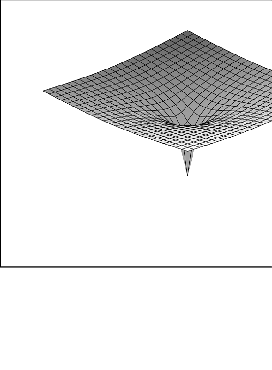
The following figure gives a two dimensional representation of what the curved space around a massive star might look like. The heavier the star, the deeper the gravitational well, and the more curved space becomes.

  

Figure 6.4: Curved Space Around a Massive Object

Einstein's General Theory of Relativity did away with all three of the above problems, and at the same time it radically altered physicists' view of the Universe. The main features of General Relativity are:

1.

Space and space-time are not rigid arenas in which events take place. They have form and structure which are influenced by the matter and energy content of the universe.

2.

Matter and energy tell space (and space-time) how to curve.

3.

Space tells matter how to move. In particular small objects travel along the straightest possible lines in curved space (space-time). (Note the above descriptions of General Relativity are due to John Wheeler.)

In curved space the rules of Euclidean geometry are changed. Parallel lines can meet, and the sum of the angles in a triangle can be more, or less than 180 degrees, depending on how space is curved. Einstein's theory gave a correct prediction for the perihelion shift of Mercury. It also explained why objects fall independent of their mass: they all follow the same straightest possible line in curved space-time. Finally, in Einstein's theory the instantaneous gravitational force is replaced by the curvature of spacetime. Moving a mass causes ripples to form in this curvature, and these ripples travel with the same speed as light. Thus, a distant mass would not feel any instantaneous change in the gravitational force, and special relativity is not violated.