Orbital Motion and Kepler's Laws

Newton originally formulate his law of gravitation to explain the motion of the planets around the sun and the orbit of the moon around the Earth. Around 1600 AD, the German astronomer Kepler was able to compile a great deal of astronomical observations into a set of three basic emperical laws that described the motion of all the planets. They are:

1.

All planets move in elliptic orbits around the Sun, with the Sun at one of the focal points of the ellipse. An ellipse is a stretched circle, as shown below.

  

Figure 6.2: Elliptic orbits

It is convenient to define the semi-major axis a of the ellipse, which is half the distance between the point of closest approach (the perihelion) and the point of farthest approach (aphelion) of the orbit. The semi-major axis can be thought of as an ``average radius'' for the orbit. The other defining characteristic of an elliptic orbit is its ``eccentricity'' which is simply the ratio of the width of the ellipse to its length. The closer the eccentricity is to one, the more circular the orbit. The shape of an orbit is completely specified if one knows the values of the semi-major axis and the eccentricity.

2.

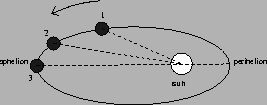
The radius vector drawn from the Sun to a planet sweeps out equal areas in equal time intervals. This implies that the planet must move slower at the furthest points of the orbit than at the closest points. For example if the planet in the Figure below moves from position 1 to 2 in the same time it takes to go from 2 to 3 (the aphelion), the areas swept out by the radius vectors (dotted lines) will only be equal if the distance from 1 to 2 is greater than from 2 to 3. Thus, the planet moves the slowest at aphelion and fastest at the perihelion. This is also consistent with energy conservation, since the planet has greatest kinetic energy when its graviational potential energy is lowest (at perihelion).

3.

The square of the orbital period, T, of any planet is proportional to the cube of the semimajor axis a of the orbit:

All three of Kepler's laws follow as direct consequence of Newton's second law, and Newton's law of gravitation. It was a major triumph of Newton's laws that they were able to explain the motion of both terrestrial objects and the motion of celestial objects.