Electrons as de Broglie waves

Returning now to the problem of the atom, it was realized that if, for the moment, we pictured the electron not as a particle but as a wave, then it was possible to get stable configurations. Imagine trying to establish a wave in a circular path about a nucleus. One possibility might be as below.

 

Figure 12.2: An unstable wave orbit

For this configuration, when one starts the wave at a given point, one ends up after one complete revolution at a different point on the wave. The incoming wave will then be out of phase with the original wave, and destructive interference will occur.

However, certain stable configurations are possible, as is illustrated below.

 

Figure 12.3: A stable wave orbit

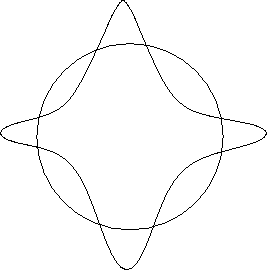In this case, the wave ends up in phase with the original wave after one complete revolution, and constructive interference results. Such a pattern would result in a stable orbit. This type of wave is called a standing wave, and are common in other contexts; for example, they can be established on a string attached to a wall if the string is moved up and down at exactly the right speed (such a wave would appear not to be moving, which is why it's called a standing wave).