Next: Acceleration Up: Motion in One Dimension Previous: Average Velocity
![]()
![]()
![]()
![]()
Next: Acceleration
Up: Motion in One Dimension
Previous: Average Velocity
Definition: Instantaneous velocity is defined mathematically:
|
v | (2) |
| t(s) | x(m) |
| 1.00 | 1.00 |
| 1.01 | 1.02 |
| 1.10 | 1.21 |
| 1.20 | 1.44 |
| 1.50 | 2.25 |
| 2.00 | 4.00 |
| 3.00 | 9.00 |
Find the runner's instantaneous velocity at t = 1.00 s. As a first estimate, find the average velocity for the total observed part of the run. We have,
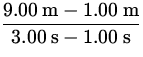 = 4 m/s. = 4 m/s.
| (3) |
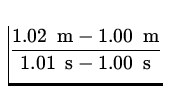 = 2 m/s. = 2 m/s.
| (4) |
We can interpret the instantaneous velocity graphically as follows. Recall
that the average velocity is the slope of the line joining P and Q (from Figure
2.1). To get the instantaneous velocity we need to take
![]() t
t ![]() 0, or P
0, or P ![]() Q.
When P
Q.
When P ![]() Q, the line joining P and Q approaches the tangent to
the curve at P (or Q). Thus the slope of the tangent at P is the instantaneous
velocity at P. Note that if the trajectory were a straight line, we would get
v =
Q, the line joining P and Q approaches the tangent to
the curve at P (or Q). Thus the slope of the tangent at P is the instantaneous
velocity at P. Note that if the trajectory were a straight line, we would get
v = ![]() , the same for all t .
, the same for all t .
Note:
www-admin@theory.uwinnipeg.ca