Nuclei

Atoms in nature generally are electrically neutral, as they have equal numbers of protons in the nucleus and orbiting electrons. However, within the nucleus there are other particles called neutrons, which are electrically neutral but have about the same mass as protons. There are two numbers used to characterize a nucleus:

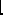$\bf$Z

, the atomic number, which equals the number of protons;

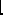$\bf$A

, the mass number, which equals the number of nucleons (protons and neutrons).

An element X is defined by the atomic number Z , while A denotes the particular isotope of that element. The usual notation for an element X is ^A_Z X - for example, there are four common isotopes of Carbon: ¹¹₆ C , ¹²₆ C , ¹³₆ C , and ¹⁴₆ C , with ¹²₆ C being the most abundant ( > 98% ).

It is convenient in some circumstances to measure masses in terms of the unified mass unit, u, which is defined so that ¹² C has a mass of 12 u exactly; in SI units,

1 u = 1.66 x 10^{- 27} kg . (1)

There is also another convenient unit of mass which arises from Einstein's Special Theory of Relativity. We have not covered this in this course, so we simply quote the relevant (well-known) relation:

 

E = mc ², (2)

which associates an energy E to a mass m , with c = 3.0 x 10⁸ m/s being the speed of light. Thus, dimensionally, E/c ² is a unit of mass. It is customary to express this unit in terms of MeV/c ², where 1 MeV=10 ⁶ eV= 1.6 x 10^{- 13} J - note that ``c'' here is considered part of the unit, and one does not substitute the numerical value of 3.0 x 10⁸ m/s in it. This will be illustrated later in some examples. Through this relation one can find the energy equivalent of 1 u:

E = (1.67 x 10^{- 27} kg )(3.0 x 10⁸ m/s )²

= 1.50 x 10^{- 10} J = 9.39 x 10⁸ eV = 939 MeV , (3)

which is then written as

1 u = 939 MeV/c ². (4)

One important illustration of the equivalence of mass and energy of Eq. (29.2) has to do with what is called the binding energy of the nucleus. It is observed that the mass of any nucleus is always less than the sum of the masses of the individual constituent nucleons which make it up. This ``loss'' of mass which then results when nucleons form a nucleus is attributed to a ``binding energy'', and is a measure of the strength of the strong force holding the nucleons together.