Next: About this document ... Up: Atomic Physics Previous: Modifications of the Bohr
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Atomic Physics
Previous: Modifications of the Bohr
![]()
If an electron makes a transition from the n = 4 to the n = 1
Bohr orbital in a hydrogen atom, determine the wavelength of
the light emitted and the recoil speed of the atom.
Solution:
To determine the wavelength, we use
![]() = R
= R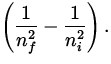
p = ![]() =
= 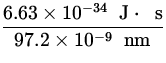 = 6.62 x 10- 27
= 6.62 x 10- 27 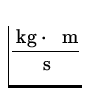 ,
,
v = ![]() =
= 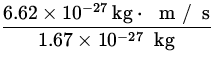 = 4.1
= 4.1 ![]() .
.
![]()
A photon incident on a hydrogen atom causes the electron to make a transition
from the n = 1 orbital to the n = 3 orbital. What is the wavelength of the
photon, and what are the possible wavelengths of the emitted radiation
when the electron returns to the n = 1 state?
Solution:
We assume the photon gives up all of its energy to the electron. In making
a transition from n = 1 to n = 3 , the electron gains an energy
E = - 13.6 eV 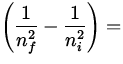 - 13.6 eV
- 13.6 eV 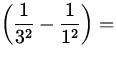 12.1 eV ,
12.1 eV ,
![]() =
= ![]() =
= 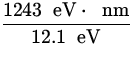 = 102.8 nm .
= 102.8 nm .
Thus, the wavelength of the incident photon is 102.8 nm, and there would be 3 possible wavelengths present in the emitted radiation when the electron returned to the n = 1 state.
![]()
An electron is in the first Bohr orbital of the hydrogen
atom. Determine
the speed of the electron, the time it takes to complete one complete
revolution, and the current in Ampères corresponding to this moving charge.
Solution:
The energy of the electron is given by
E = - ![]() = -
= - 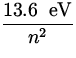 ,
,
![]() =
= ![]() mv 2,
mv 2,
![]() mv 2 = - E = 13.6 eV x
mv 2 = - E = 13.6 eV x 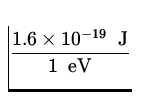 = 2.2 x 10- 18 J .
= 2.2 x 10- 18 J .
v = 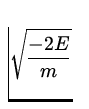 =
= 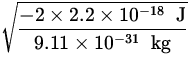 = 2.2 x 106
= 2.2 x 106 ![]() .
.
T = 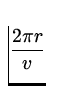 =
= 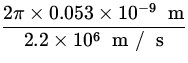 = 1.52 x 10- 16 s .
= 1.52 x 10- 16 s .
I = ![]() =
= ![]() =
= 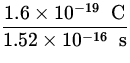 = 1.1 x 10- 3 A .
= 1.1 x 10- 3 A .
![]()
Consider a string fixed at both ends which vibrates in a standing wave
pattern, as in Fig. 28.3.
Suppose such a wave pattern describes a free particle of mass m confined to a box of length L . Find the allowable energy levels of such a particle.
Solution:
In order for a standing wave to exist between the ends, we must have
a half integral or else an integral number of wavelengths present:
n![]() = L
= L![]()
![]() n = 1,2,3,...
n = 1,2,3,...
![]() =
= ![]() =
= ![]()
![]() v =
v = ![]() .
.
En = ![]() mv 2 =
mv 2 = 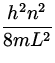 .
.
![]()
Write out the possible electronic energy states for an electron
in the n = 1 and 2 energy levels.
Solution:
For a given value of n , the orbital quantum number can assume
values
l = 0,1,2,...,n - 1 , the orbital magnetic quantum
number can be
ml = - l, - l + 1,...,0,...,l - 1,l , and the spin
quantum number can be
ms = ![]()
![]() .
.
For n = 1 we have only l = 0 , for which ml = 0 is the only allowed value. Thus, we find
For n = 2 , l can assume values 0 (with ml = 0 ) or 1 (for which ml = - 1,0,1 ). We then have
| n | l | ml | ms |
| 2 |
- |
||
| 2 |
+ |
||
| 2 | 1 | - 1 |
- |
| 2 | 1 | - 1 |
+ |
| 2 | 1 |
- |
|
| 2 | 1 |
+ |
|
| 2 | 1 | + 1 |
- |
| 2 | 1 | + 1 |
+ |
Note that at this point we cannot say which of the various states for a given value of n have lower energy.
www-admin@theory.uwinnipeg.ca