Escape Velocity

Escape velocity is defined as the smallest speed that we need to give an object in order to allow it to completely escape from the gravitational pull of the planet on which it is sitting. To calculate it we need only realize that as an object moves away from the center of a planet, its kinetic energy gets converted into gravitational potential energy. Thus we need only figure out how much gravitational potential energy an object gains as it moves from the surface of the planet off to infinity. According to the above discussion for a planet with mass M and radius R, this gain in gravitational potential energy is GmM/R. For an object to just barely escape to infinity (without any residual speed), all its initial kinetic energy must go into this increase in gravitational potential energy. Thus, the initial kinetic energy must be equal to GmM/R. Since kinetic energy is mv²/2, equating these two expressions tells us that the square of the initial velocity must be equal to twice the gravitational potential energy divided the inertial mass of the object. However, since gravitational potential energy is proportional to inertial mass, we find finally that the square of the escape velocity depends only on the mass and radius of the planet (and of course Newton's gravitational constant):

v² = $${2GM\over R}$$

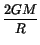
Note that the inertial mass of the object has cancelled, so that the escape velocity of any object is independent of its mass. This means that if you want to throw a grain of rice or an elephant into outer space, you need to give them both the same initial velocity which for the Earch works out to be about 10,000 meters per second.

You will also notice from the above expression that if the mass of a planet or star stays fixed, but its radius decreases, then the escape velocity necessarily increases. This will play an important role in our discussion of black holes later in this chapter.