Gravitational Potential Energy

As discussed in a previous chapter, gravity is a conservative force so that we can assign gravitational potential energy to any object moving under the influence of gravity. However, in the previous discussion the gravitational acceleration of the object was assumed constant, and we now know that this is only approximately true for objects that move through vertical distances that are small compared to the radius of the Earth. More generally, (for example for satellite orbits) we must take into account the fact that the gravitational acceleration changes as the object moves. Instead of graviational potential energy being simply proportional to the height above the Earth's surface, one finds that it is inversely proportional to the distance from the object to the center of the Earth. It is reasonable that gravitational potential energy depends on Newton's constant and the Earth's mass in the same way that the gravitational force does. The correct expression for gravitational potential energy for an object a distance r from the center of the Earth is:

U = - $${G M_E m\over r}$$

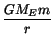
The minus sign ensures that the potential energy decreases (gets more and more negative) as the object falls towards the center of the Earth. The dependence of the gravitational potential energy U on the distance r from the center of the Earth is illustrated in the Figure below.

  

Figure 6.1: Gravitational Potential Energy

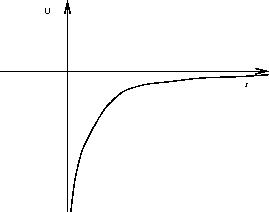Notice that the gravitational potential energy has been defined so that an object very far from Earth's center (i.e. infinite r) has zero potential energy. This observation enables us to calculate in a simple way the escape velocity of any object sitting on the Earth.