




Next: Space Travel
Up: Other Implications of Special
Previous: Other Implications of Special
One thing you will notice about the procedure defined at the end of
the previous Section 11.5 is that the gain when you try to
accelerate a ball to the speed of light in steps, the increase
in velocity relative to the initial frame gets less and less, each
time you repeat the process. The faster the ball is going, the hard it is to
accelerate further. Now recall the definition of inertial
mass: it is the measure of an object's resistance to a
change in motion. In Newtonian physics inertial mass is a property of
the object alone, and does not depend in any way on its state of
motion. A one kilogram ball has a mass of one kilogram no matter how
fast it happens to be moving. The situation is drastically
different in Special Relativity. The faster a mass moves, the harder it
is to accelerate. Hence its inertial mass depends on its speed! It will come
as no surprise that this dependence is determined by the time dilation
factor 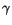 . In particular, if an object is moving relative to you
at a speed of v, you will measure an inertial mass that increases by
a factor of
. In particular, if an object is moving relative to you
at a speed of v, you will measure an inertial mass that increases by
a factor of 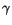 compare to its value m0 at rest:
compare to its value m0 at rest:
m =  m0 m0
|
(11.14) |
m0 is called the rest mass of the object, for obvious reasons.
For example, if an object is moving at .99c, its mass
will appear to be a factor of seven times larger than its rest
mass. Again,
because of the form of 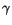 this effect is
negligible at velocities that are small compared to the speed of
light.
However, the increase of inertial mass with velocity has been measured in
the large accelerators used by particle physicists to create fast
moving beams of electrons. The faster the electrons are moving, the
harder it is to further increase their kinetic energy.
this effect is
negligible at velocities that are small compared to the speed of
light.
However, the increase of inertial mass with velocity has been measured in
the large accelerators used by particle physicists to create fast
moving beams of electrons. The faster the electrons are moving, the
harder it is to further increase their kinetic energy.
There is another profound implication of the above considerations that
Einstein was the first to realize. We know that when you increase the
velocity of an object, you are giving it kinetic energy. We also know
that kinetic energy can be converted into other forms of energy, such
as potential energy and heat energy and vice versa. If increasing the velocity of an
object
increases its
inertial mass, then in some sense we are converting kinetic
energy into mass. Einstein reasoned that mass and energy must somehow
be different manifestations of the same thing. In particular if we can convert
kinetic energy into mass, we should also be able to convert mass into
energy.
The special theory of relativity in fact gives an explicit expression
for how mass and energy are related. You have probably seen it before.
E = mc2 = m0 c2 c2
|
(11.15) |
Thus as expected from earlier objects, the energy of an object
increase without bound as its velocity approaches the speed of light.
The surprising aspect of 11.15 is that even when an object
is at rest, it has energy. When v = 0, 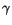 = 1 amd m = m0 so that
for a mass at rest:
The energy of an object at rest is related to its mass by the factor
c2 which is a very large number. The consequence is that very small
masses can produce vast amounts of energy, and nuclear power plants
and bombs are effective because they can convert mass into other forms
of energy. In fact, if all the mass in a single grain of sand could be
converted into energy, it could provide enough electricity to light up
a whole city for a year. As we will see in the Section on Nuclear
Physics, however, it is not easy to convert large amounts of mass into
energy.
= 1 amd m = m0 so that
for a mass at rest:
The energy of an object at rest is related to its mass by the factor
c2 which is a very large number. The consequence is that very small
masses can produce vast amounts of energy, and nuclear power plants
and bombs are effective because they can convert mass into other forms
of energy. In fact, if all the mass in a single grain of sand could be
converted into energy, it could provide enough electricity to light up
a whole city for a year. As we will see in the Section on Nuclear
Physics, however, it is not easy to convert large amounts of mass into
energy.





Next: Space Travel
Up: Other Implications of Special
Previous: Other Implications of Special
modtech@theory.uwinnipeg.ca
1999-09-29