Definitions of Physical Quantities

  

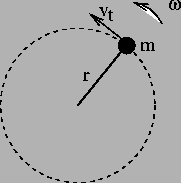
Figure 1: Circular Motion

Angular Velocity:

$$\omega={d\theta\over dt}={v_t\over r}$$

Angular Acceleration:

$$\alpha = {d\omega\over dt} = {a_t\over r}$$

Period:

$$T={2\pi r\over v_t} = {2\pi\over \omega}$$

Centripetal Acceleration:

$$a_c = {v_t^2\over r}$$

Rotational Kinetic Energy:

$${\rm KE}_{{\rm rot}}= {1\over 2} mv_t^2 = {1\over 2} m(r\omega)^2 = {1\over 2} I \omega^2$$

Moment of Inertia about a Given Axis of Rotation:

I = mr²

Torque

$$\tau = r F_{\perp}= rF \sin(\theta)= I\alpha= {d L\over dt}$$

Angular Momentum

$$L= I \omega = m v_t r$$

NOTE:

• Angular velocity, angular acceleration, torque and angular momentum are vector quantities. The above formulas give their magnitudes. Their directions are always perpendicular to the plane of rotation, with the actual direction determined by the right hand rule: curl the fingers of your right hand along the direction of rotation, and your thumb points along the direction of the corresponding vector.

• Moment of inertia, torque, angular momentum are always defined relative to a given axis of rotation. Different choices of axis give different values of these quantities for the same mass moving with the same linear velocity.