Next: About this document ... Up: Rotational Equilibrium and Dynamics Previous: Problem Solving Strategies
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Rotational Equilibrium and Dynamics
Previous: Problem Solving Strategies
Solution:
![]()
![]() =
= ![]() mssg - xmcg = 0
mssg - xmcg = 0
x =  =
= 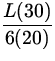 =
= ![]() L.
L.
![]()
![]() =
= ![]() mssg -
mssg - ![]() mcg = 0
mcg = 0
mc = ![]() mss =
mss = ![]() (30) = 15 kg.
(30) = 15 kg.
![]()
A 10 m ladder weighs 50 N and balances against a smooth wall at
60 o to the horizontal. If the ladder is just on the verge
of slipping,
what is the static coefficient of friction between the floor and
the ladder?
Solution:
The force diagram for the ladder is shown in
Figure 8.4.
We need to impose both equilibrium conditions: i)
![]()
![]() = 0
and ii)
= 0
and ii)
![]()
![]() = 0.
= 0.
|
| = | fs - N1 | |
|
| = |
| |
|
[2mm] | = | N2 - mg | |
|
| = | mg |
0 = ![]() mg - N1.
mg - N1.
|
| = |
- mg(L/2)cos | |
|
| = |
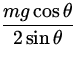 . .
|
| = |
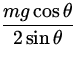
| ||
|
| = |
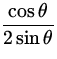 = =  = 0.29 = 0.29
|
![]()
Calculate the x and y positions of the center of mass of the
following
three objects where
m1 = 1.0 kg ,
m2 = 2.5 kg , and
m3 = 4.0 kg . See
Figure 8.5.
Solution:
| xcm | = |
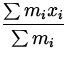
| |
| = |
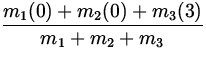 = 1.6 m = 1.6 m
| ||
| [2mm]ycm | = |
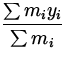
| |
| = |
 = 0.27 m. = 0.27 m.
|
![]()
Calculate the moments of inertia of the following 4 masses where
m1 = 2.0 kg and
m2 = 1.0 kg. See Figure 8.6.
a) About the axis through O (center) perpendicular to the page.
b) About an axis joining two of the masses.
Note: The moment of inertia depends strongly on the axis chosen.
Solution:
| IO | = |
| |
| = | 2m1(22) + 2m2(32) | ||
| = | 8m1 + 18m2 | ||
| = | 34 kg m 2. |
First consider the x -axis (i.e. the one that passes through the
m2 's):
| Ix | = |
| |
| = | m1(22) + m2(02) + m1(22) + m2(02) | ||
| = | 2m1(22) = 16 kg m 2. |
For the y -axis (i.e. the one that passes through the two
m1 's):
| Iy | = |
| |
| = | m1(0) + m2(32) + m1(0) + m2(32) | ||
| = | 2m2(32) = 18 kg m 2. |
![]()
A round object, mass m , radius r and moment of inertia IO ,
rolls down a ramp without
slipping as shown in Fig. 8.6 below.
a) If the ramp is at an angle
![]() to the horizontal, find an expression for
the acceleration of the center
of mass of
the object in terms of m,r,I0 and
to the horizontal, find an expression for
the acceleration of the center
of mass of
the object in terms of m,r,I0 and ![]() . b) What is the
velocity of the center of mass of a
solid sphere,
IO =
. b) What is the
velocity of the center of mass of a
solid sphere,
IO = ![]() mr 2, if
it starts from rest and rolls down a 4 m ramp inclined at
30 o to the
horizontal?
mr 2, if
it starts from rest and rolls down a 4 m ramp inclined at
30 o to the
horizontal?
Solution:
|
| = |
mgsin | |
|
| = |
gsin | |
|
[2mm] | = |
N - mgcos |
For the rotational motion we have:
|
| = | - fsr | |
|
| = |
 . .
|
acm = - at = - r![]() .
.
fs = 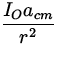 .
.
acm = gsin ![]() - IO
- IO![]()
acm = 
| vx | = |

| |
| = |

| ||
| = | 5.3 m/s. | (17) |
Note that the mass and radius of the object cancel out of the final expression.
acm = gsin ![]()
![]()
Do the above problem (part b) using energy conservation.
Solution:
| Wnc = 0 | = |
| |
| = |
( | ||
|
| = |
mvcm2 + I |
h = Lsin ![]() (fromthediagram)
(fromthediagram)
|
| = |
| |
| I sphere | = |
|
| = |
mvcm2 + ( | ||
| = |
5vcm2 + 2vcm2 - 10gLsin | ||
|
| = |
 = 5.3 m/s = 5.3 m/s
|
![]()
A cylinder with moment of inertia
I = 34 kg m 2 rotates
at
![]() = 1.4 rads/s .
It drops onto a second identical cylinder, and they stick
together end to end. a) Calculate the final angular velocity of
the two
cylinders. b)
Calculate the kinetic energy lost in the process.
= 1.4 rads/s .
It drops onto a second identical cylinder, and they stick
together end to end. a) Calculate the final angular velocity of
the two
cylinders. b)
Calculate the kinetic energy lost in the process.
Solution:
|
I | = |
I | |
|
I | = |
2I | |
|
| = |
|
|
| = | KErf - KEri | |
| = |

| ||
| = |
I
| ||
| = | - 16.7 J |
![]()
A student stands on the center of a rotating platform that has
frictionless
bearings. He has a 2.0 kg object in each hand, held 1.0 m from the
axis of
rotation of the system. The system is initially rotating at 10
rpm.
Determine a) the initial angular velocity in radians per second,
b) the
angular velocity of the sytem in radians per second after the
objects are
brought to a distance of 0.20 m from the axis of rotation, c) the
change in
the rotational kinetic energy of the system as the objects are
pulled closer
to the center of rotation. d) What causes the increase in
rotational kinetic
energy? (Assume that the moment of inertia of the platform +
student remains
constant at 1.0 kg m 2.)
Solution:
| 10 rev/min | = |
(10 rev/min )(2 | |
| = | 1.05 rad /s. |
| Ii | = | I (student + platform) + mri2 + mri2 | |
| = | 1.0 kg m 2 + (2.0 kg )(1.0 m )2 + (2.0 kg )(1.0 m )2 | ||
| = | 5.0 kg m 2 |
| If | = | I (student + platform) + mrf2 + mrf2 | |
| = | 1.0 kg m 2 + (2.0 kg )(0.2 m )2 + (2.0 kg )(0.2 m )2 | ||
| = | 1.16 kg m 2. |
|
Ii |
|
| = |
| |
| = |
| ||
| = | 4.5 rads/s. |
|
| = | KEf - KEi | |
| = |
| ||
| = |
| ||
| = | 11.8 J - 2.75 J | ||
| = | 9.05 J. |
www-admin@theory.uwinnipeg.ca