



Next: Nuclear Reactions
Up: Nuclear Physics
Previous: Radioactivity
The radioactivity of a substance is measured by how many decays per
unit time occur. Two popular units of the activity
are used: the curie (Ci),
defined as
|
1 Ci = 3.7 x 1010 decays/s
| (8)
|
and the becquerel (Bq), defined as
Note that, by themselves, these units do not measure accurately
how dangerous a given amount of
radiation might be for humans - for medical purposes
other units of radioactivity reflecting this aspect are more appropriate.
It is found that, if a given radioactive substance at a certain time
contains N nuclei, then at a short time  t later a certain
number
t later a certain
number  N have decayed which is given by
N have decayed which is given by
where  is called the decay constant. Note that
is called the decay constant. Note that  has units of inverse time, or s - 1.
The decay rate,
R , is defined as the number of decays per unit time:
has units of inverse time, or s - 1.
The decay rate,
R , is defined as the number of decays per unit time:
|
R =  = = 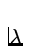 N. N.
| (11)
|
For finite times it is found that the number of nuclei present after
a time t is given by
|
N = N0e -  t t
| (12)
|
where N0 is the number of nuclei present at t = 0 and
e = 2.71828...
is the base of the ``natural'' logarithms (compared to the base 10 of the
``common'' logarithms). Thus, from Eq. (29.12),
in a time t =  a fraction
e - 1 = 0.36787944... of a substance remains.
a fraction
e - 1 = 0.36787944... of a substance remains.
It is sometimes convenient to introduce the half-life, T1/2 , of a
substance, defined as the time over which exactly one half of a substance
remains. From Eq. (29.12) one finds
where
ln 2 = 0.693... is the natural logarithm of 2 (note
ln e = 1 , which is analogous to log 10 = 1 for the common
logarithm). In terms of
the half-life Eq. (29.12) can be written as
|
 = =  t/T1/2. t/T1/2.
| (14)
|
Thus, after a period of one half-life  of a substance remains,
after another half life
of a substance remains,
after another half life
 x
x  =
= 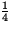 of a substance remains, and so on. Half-lives of
substances range from tiny fractions of a second to millions of years.
of a substance remains, and so on. Half-lives of
substances range from tiny fractions of a second to millions of years.




Next: Nuclear Reactions
Up: Nuclear Physics
Previous: Radioactivity
www-admin@theory.uwinnipeg.ca
10/9/1997
![]()
![]()
![]()
![]()
![]() t later a certain
number
t later a certain
number ![]() N have decayed which is given by
N have decayed which is given by
 =
=