Next: About this document ... Up: Magnetism Previous: Force between two parallel
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Magnetism
Previous: Force between two parallel
![]()
What is the net force (magnitude and direction) on
the electron moving in the magnetic field in Fig. 1.10
if B = 2 T,
v = 4 x 104 m/s, and
![]() = 30 o ?
= 30 o ?
Solution:
We first find the magnitude of the force as
F = qvBsin ![]() = 1.6 x 10- 19
= 1.6 x 10- 19 ![]() 4 x 104
4 x 104 ![]() 2
2 ![]() sin 30 o = 6.4 x 10- 15 N .
sin 30 o = 6.4 x 10- 15 N .
![]()
Suppose a very long straight wire of linear mass
density 20 g/m is immersed in a constant magnetic
field B = 3 T, as in Fig. 1.11. What current I would be
required so that the wire will be suspended?
Solution:
We note that the force per unit length due to gravity,
![]() =
= ![]() g,
g,
![]() = IB,
= IB,
![]() g = IB
g = IB ![]() I =
I = ![]()
![]() =
= 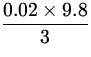 = 0.065 A .
= 0.065 A .
![]()
Consider the mass spectrometer in Fig. 1.12. The electric field
between the plates of the velocity selector is E = 950 V/m,
and the magnetic field B in both the velocity selector and
in the deflection chamber has a magnitude of 0.9 T.
Find the radius r for a singly charged ion of mass
m = 2.18 x 10- 26 kg in the deflection chamber.
Solution:
We first use the fact that in order for the ion to pass
through the velocity selector undeflected the force due
to the electric and magnetic fields must balance. Note that
the force on a positive charge is downwards due to the electric
field and upwards due to the magnetic field; to balance,
we then have
qE = qvB ![]() v =
v = ![]() .
.
F = qvB = m![]()
![]() qB =
qB = ![]() .
.
r = ![]() v =
v = 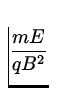 =
= 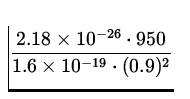 = 1.6 x 10- 4 m .
= 1.6 x 10- 4 m .
![]()
The two long straight
wires in Fig. 1.13 each carry a current of I = 5 A
in opposite directions
and are separated by a distance d = 30 cm. Find the magnetic
field a distance l = 20 cm to the right of the wire on the
right.
Solution:
We shall use the expression for the magnetic field
of a long straight wire a distance r away as
B = ![]() ,
,
BR = ![]() =
= 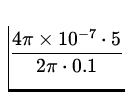 = 1.0 x 10- 5 T ,
= 1.0 x 10- 5 T ,
BL = 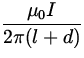 =
= 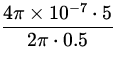 = 2.0 x 10- 6 T ,
= 2.0 x 10- 6 T ,

For the arrangement shown in Fig. 1.14,
the long straight wire carries a
current of I1 = 5 A. This wire is a distance d = 0.1 m away from
a rectangular loop of dimensions a = 0.3 m and b = 0.4 m which
carries a current I2 = 10 A. Find the net force exerted on the
rectangular loop by the long straight wire.
Solution:
The force
![]() = l
= l![]() x
x ![]() on the rectangular
loop arises due to the magnetic field
B =
on the rectangular
loop arises due to the magnetic field
B = ![]() I/2
I/2![]() r of the
long straight wire. We first of all note that the force
cancels between the top and bottom portions of the loop.
Now, on the left
portion of the loop,
r of the
long straight wire. We first of all note that the force
cancels between the top and bottom portions of the loop.
Now, on the left
portion of the loop,
BL = ![]() ,
,
FL = bI2BL = 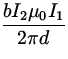 =
= 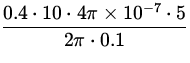 = 4 x 10- 5 N ,
= 4 x 10- 5 N ,
BR = 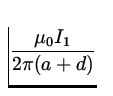 ,
,
FR = bI2BR = 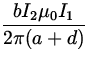 =
= 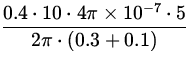 = 1 x 10- 5 N ,
= 1 x 10- 5 N ,
www-admin@theory.uwinnipeg.ca