Next: About this document ... Up: Force Previous: Problem Solving Strategy
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Force
Previous: Problem Solving Strategy
![]()
A box of mass 5.0 kg is pulled vertically upwards by a force of
68 N applied to a rope attached to the box. Find a) the acceleration of the
box
and b) the vertical velocity of the box after 2 seconds.
Solution:
| ma | = | T - mg | |
|
| = |
| |
| = |
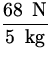 - 9.8 m/s 2 = 3.8 m/s 2 - 9.8 m/s 2 = 3.8 m/s 2
| (5) |
| v | = | v0 + at | |
| = | 0 + 3.8(2) = 7.6 m/s. | (6) |
![]()
A hockey puck of mass .5 kg travelling at 10 m/s slows to 2.0 m/s over a
distance of 80 m. Find a) the frictional force acting on the puck
and b) the coefficient of kinetic friction between the puck and the surface.
Solution:
| v 2 | = | v02 + 2ax | |
|
| = |
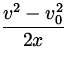 = = 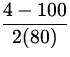 = - 0.6 m/s 2 = - 0.6 m/s 2
| (7) |
| fk = ma = .5(- 0.6) = - 0.3 N. | (8) |
|
- | = | ma | |
|
| = | - a/g | |
| = | 0.061. | (9) |

A student of mass 50 kg tests Newton's laws by standing on a
bathroom scale in an elevator. Assume that the scale reads in newtons. Find
the scale reading when the elevator is a) accelerating upward at .5 m/s 2, b)
going up at a constant speed of 3.0 m/s and c) going up but decelerating at
1.0 m/s 2.
Solution:
From the 2nd Law:
| Fs - mg | = | ma | |
|
| = | m(g + a). | (10) |
![]()
A wooden plank is raised at one end to an angle of 30 o .
A 2.0 kg box is placed on the incline 1.0 m from the lower end and given a
slight tap to overcome static friction. The coefficient of kinetic friction
between the box and the plank is
![]() = 0.20 . Find a) the rate of acceleration of the
box and b) the speed of the box at the bottom. Assume that the initial speed
of the box is zero.
= 0.20 . Find a) the rate of acceleration of the
box and b) the speed of the box at the bottom. Assume that the initial speed
of the box is zero.
Solution:
| wx | = |
- mgsin | |
| wy | = |
- mgcos |
| x |
: - mgsin | ||
| y |
: N - mgcos | (11) |
| ma | = |
- | |
|
| = |
g(sin | |
| = | 9.8(sin 30 - 0.2cos 30) = 3.20 m/s 2 | (12) |
|
v = |

A 10 kg box is attached to a 7 kg box which rests on a
30 o incline. The coefficient of kinetic friction between each box and
the
surface is ![]() = .1 . Find a) the rate of acceleration of the system and b) the
tension in the rope.
= .1 . Find a) the rate of acceleration of the system and b) the
tension in the rope.
Solution:
We apply the 2nd law separately to each box.
For the 10 kg box:
y direction:
| N2 - m2g | = | ||
| N2 | = | m2g, |
| T - fk 2 | = | m2a | |
|
T - | = | m2a | |
|
| = | m2a. | (13) |
|
N1 = m1gcos |
|
m1gsin | = | m1a | |
|
m1gsin | = | m1a | |
|
| = | m1a. | (14) |
We have a system of two equations and two unknowns: a and T . We can
solve
as follows.
| m1a | = |
m1gsin | |
|
| = |
m1gsin | (15) |
|
| = |
| |
| = |
| (16) |
| T | = |
m2(a + g | |
| = | 10(9.8(.1) + 1.1) = 20.8 N. | (17) |
www-admin@theory.uwinnipeg.ca