



Next: Problems
Up: Solids and Fluids
Previous: Buoyant Forces
Idea: Since the motion of fluids can be very complicated
(due to turbulence, frictional forces between molecules etc.) we
need to make the following simplifying assumptions:
- No internal friction between layers of fluid (zero
viscosity).
- The density of the fluid remains the same throughout the
fluid
(non-compressibility).
- Fluid velocity and pressure at each point in the fluid do not
change with time (steady state).
- The fluid particles follow smooth, predictable flow lines
(streamline or laminar flow).
Definition: Flow Rate
The flow rate at each point along a (non-uniform)
pipe or hose is defined as the volume of fluid passing through the
pipe at that point per unit time:
|
FlowRate =  = A = A = Av = Av
| (15)
|
where A is the cross-sectional area of the pipe at that point
and
v = 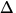 x/
x/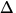 t is the fluid velocity.
t is the fluid velocity.
Idea: If the fluid is incompressible, the
flow rate must be the same everywhere along the pipe (Conservation
of fluid particles: what goes in must come out). This leads
directly to the Continuity Equation:
Idea: Conservation of energy requires that the work done in
moving a volume of fluid through a portion of pipe must go into
kinetic energy
and/or potential energy of the fluid (assuming no frictional
forces). Consider a fluid moving through a pipe as in Fig.9.8.
Figure 9.8:
Fluid motion
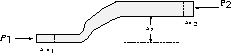 |
The work done by the pressure P1 on the left
in moving the fluid a distance  x1 is:
x1 is:
W1 = F1x1 = P1A1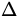 x1.
x1.
On the right, the work done by the pressure is:
W2 = - F2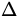 x2 = - P2A2
x2 = - P2A2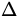 x2
x2
where the minus sign occurs because the force is in the opposite
direction of
the motion in this case. By the continuity equation, the amount
of fluid
entering the pipe on the left must equal the amount leaving on the
right.
Thus:
A1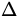 x1 = A2
x1 = A2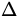 x2.
x2.
This volume of fluid, which we call V , can undergo both a change
in kinetic
energy and a change in potential energy as it is pushed through the
pipe:
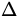 KE KE
|
=
|
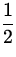 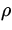 Vv22 - Vv22 - 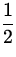 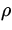 Vv12 Vv12
| |
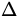 PE PE
|
=
|
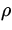 Vgy2 - Vgy2 - 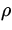 Vgy1. Vgy1.
| |
Equating the work done ( W = W1 + W2 ) to the change in mechanical
energy
(
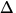 KE +
KE + 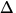 PE ) leads directly to
Bernouilli's Equation (note that the volume
V = A1
PE ) leads directly to
Bernouilli's Equation (note that the volume
V = A1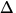 x1 = A2
x1 = A2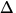 x2 cancels):
x2 cancels):
|
P1 + 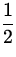 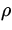 v12 + v12 + 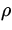 gy1 = P2 + gy1 = P2 + 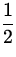 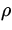 v22 + v22 + 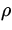 gy2 gy2
| (17)
|
where P1 , v1 and y1 are the pressure, fluid velocity and
height of the fluid at one end, etc.
Note: If there is no height difference, Bernouilli's equation
relates the pressure at two points along the flow to the fluid
velocities:
|
P1 - P2 = 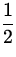 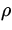 (v22 - v12). (v22 - v12).
| (18)
|
Thus, pressure in the fluid decreases whenever the
fluid velocity increases. This results in important observable
effects, such as the lift produced by an airplane wing, the curving
of a
spinning baseball and the fact that the shower curtain gets sucked
in when you first turn on the shower.




Next: Problems
Up: Solids and Fluids
Previous: Buoyant Forces
www-admin@theory.uwinnipeg.ca
10/9/1997
![]()
![]()
![]()
![]()
![]() x1 is:
x1 is:
![]() x1.
x1.
![]() x2 = - P2A2
x2 = - P2A2![]() x2
x2
![]() x1 = A2
x1 = A2![]() x2.
x2.