Next: About this document ... Up: Circular Motion and the Previous: Newton's Law of Gravitation
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Circular Motion and the
Previous: Newton's Law of Gravitation
![]()
A bicycle wheel of radius
r = 1.5 m starts from rest and
rolls 100 m without slipping in 30 s. Calculate a) the number of
revolutions the wheel makes, b) the number of radians through which
it turns, c)The average angular velocity.
Solution:
n = =  = 10.6.
= 10.6.
![]()
![]() = 2
= 2![]() n =
n = ![]() =
= 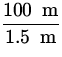 = 66.7 radians.
= 66.7 radians.
![]() =
= ![]() =
=  = 2.22 rads/s.
= 2.22 rads/s.

Assuming that the angular acceleration of the wheel given
above was constant, calculate: a) The angular acceleration, b) the
final angular velocity c) the tangential velocity and tangential
acceleration of a point on the rim after one revolution.
Solution:
![]()
![]() =
= ![]()
![]() t +
t + ![]()
![]() (
(![]() t)2.
t)2.
![]() =
=  =
=  = 0.15 rads/s 2.
= 0.15 rads/s 2.
![]() =
= ![]() +
+ ![]()
![]() t = 0 + (0.15)(30) = 4.5 rads/s.
t = 0 + (0.15)(30) = 4.5 rads/s.
![]() = 2
= 2![]()
![]()
![]() +
+ ![]()
![]() =
=  = 1.37 rads/s.
= 1.37 rads/s.
vt = r![]() = (1.5 m )(1.37 rads/s ) = 2.06 m/s
= (1.5 m )(1.37 rads/s ) = 2.06 m/s
at = r![]() = (1.5 m )(0.15 rads/s 2) = .225 m/s 2.
= (1.5 m )(0.15 rads/s 2) = .225 m/s 2.
![]()
A yo-yo of mass 100 g is spun in a vertical circle at
the end of a 0.8 m string at a constant angular velocity of
4 rads/s.
Calculate a) the tension in the string at the top of its
trajectory, b) the tension in the string at the bottom of the
trajectory.
Solution:
mac = T + mg
so that| T | = |
mr | |
| = | .1 kg x .8 m x (4 rads/s )2 - .1 kg x 9.8 m/s 2 = 0.3 N. |
mac = T - mg
so that
T = mac + mg = mr![]() + mg = 2.26 N.
+ mg = 2.26 N.
![]()
The same yo-yo as in the previous problem is spun in a horizontal
circle, as shown in Figure 7.5.
If the string makes an angle of 30 o to the vertical, what is the period of rotation?
Solution:
Apply Newton's Laws of Motion:
m![]() =
= ![]() +
+ ![]() .
.
Vertical:
0 = Tcos ![]() - mg.
- mg.
T = ![]() = 1.13 N.
= 1.13 N.
Horizontal:
| mac | = |
Tsin | |
|
| = |
Tsin |
![]() =
= 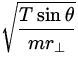
![]() =
=  = 3.76 rads/s.
= 3.76 rads/s.
T = ![]() = 1.67 s.
= 1.67 s.
Note: as
![]()
![]() 90 o , T
90 o , T![]()
![]() in order to
balance the gravitational force, so that the period
in order to
balance the gravitational force, so that the period ![]() 0: i.e.
you must spin it infinitally fast to get it to be horizontal. Try
it!
0: i.e.
you must spin it infinitally fast to get it to be horizontal. Try
it!
![]()
What is the relationship between the radius of orbit of a
satelite (mass m ) and its period?
Solution:
The centripetal force is provided by
the gravitational pull of the Earth, which is the only force acting
on the satellite
Newton's Second Law is therefore:
|
| = |
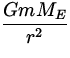
| |
|
mr | = |
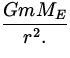
|
![]() =
= 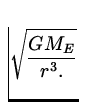
T = ![]() = .
= .
![]()
The escape velocity of any object is the speed it must
achieve to escape the gravitational pull of the Earth. Calculate
the escape velocity for an object of mass m .
Solution:
We can use conservation of mechanical energy (neglecting air
resistance):
KEf + PEf = KEi + PEi.
Suppose the object starts at the earth's surface with speed vE and reaches r =
0 = ![]() mvE2 -
mvE2 - 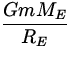
vE = 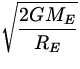 .
.
vE = 11 km/s
Note:
vE = 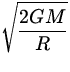 .
.
Rc = 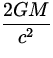 .
.
www-admin@theory.uwinnipeg.ca