



Next: Other Atoms
Up: Atomic Physics
Previous: Atomic Spectra
The first successful model of hydrogen was developed by Bohr in 1913,
and incorporated the new ideas of quantum theory. The major success of
this model was an explanation of the simple formula (28.1) for the
emission spectra. The arguments begin with considering the electron orbiting
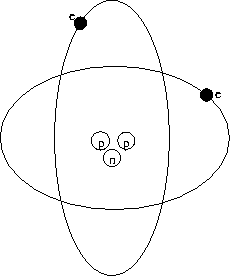
around the proton, as in the planetary model sketched in
Fig. 28.1.
Figure 28.1:
Planetary model of the atom
 |
Such an electron will have a
kinetic energy,
|
KE =  mv 2, mv 2,
| (3)
|
and an electrical potential energy
so that the total energy is
|
E =  mv 2 - k mv 2 - k  . .
| (5)
|
Now, from Newton's 2
nd law, we know that the Coulomb
force supplies the centripetal acceleration:
so that the total energy of Eq.(28.5) becomes
|
E = - k  . .
| (7)
|
Up until this point the analysis has been classical, and as such the model
suffers from the instability problem mentioned previously. What Bohr did
was to now consider the electron not as a particle but as a wave, with
wavelength given by de Broglie's relation:
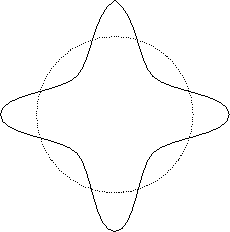
Furthermore, if one tries to ``wrap'' such a wave around
a circular orbit about the proton, as in
Fig. 28.2,
Figure 28.2:
Stable electron wave orbital
 |
then only certain wavelengths would be allowed for a stable orbit:
Combining this with Eq.(28.8), we see that this quantization
condition becomes
where

 h/2
h/2 . This then
says that the angular momentum of the electron is quantized
in units of
. This then
says that the angular momentum of the electron is quantized
in units of  .
.
If one combines Eqs.(28.6,28.10), one sees
|
v 2 =  = =   rn = rn =  n 2 n 2  a n 2, a n 2,
| (11)
|
where
|
a0 =  = 0.053 nm = 0.053 nm
| (12)
|
is a constant called the first Bohr radius. Thus, in this model
only certain radii rn satisfying Eq.(28.11) are allowed for
stable orbits. Corresponding to these orbits are discrete energy
levels; one finds
Thus, the electrons in this model are confined to certain orbits with
definite energies. Let us consider what happens when an electron in
a high energy orbit n = ni falls to a lower energy state with
n = nf , where ni > nf . Such a process in itself would not conserve
energy; let us postulate that the excess energy is carried away by a
photon of energy
hf = hc/ . Energy conservation then tells us
. Energy conservation then tells us
which is of the same form as Eq.(28.1) for the hydrogen
spectra, and also gives an expression for Rydberg's constant
(28.2) in terms of known quantities:
|
RH =  = 1.097 x 107 m - 1. = 1.097 x 107 m - 1.
| (15)
|
This provides excellent agreement with experiment, and was a major
success of the early quantum theory.




Next: Other Atoms
Up: Atomic Physics
Previous: Atomic Spectra
www-admin@theory.uwinnipeg.ca
10/9/1997
![]()
![]()
![]()
![]()
 = - k
= - k  n 2
n 2  = 0.053 nm
= 0.053 nm

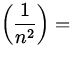 -
- ![]() . Energy conservation then tells us
. Energy conservation then tells us


 = 1.097 x 107 m - 1.
= 1.097 x 107 m - 1.