Electric field

A convenient concept for describing electric forces is that of an electric field. Imagine that we have a fixed distribution of charges, such as on the plate below, and bring in the vicinity of this distribution a test charge Q.

 

Figure 9.2: Test charge in the presence of a fixed charge distribution

This charge will experience a force due to the presence of the other charges. One defines the electric field of the charge distribution as

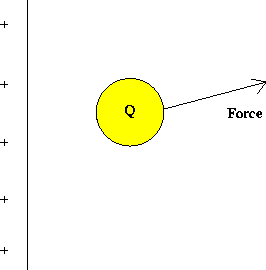
The electric field is a property of this fixed charge distribution; the force on a different charge Q' at the same point would be given by the product of the charge Q' and the same electric field. Note that the electric field at Q is always in the same direction as the electric force.

  Because the force on a charge depends on the magnitude of the charges involved and on the distances separating the charges, the electric field varies from point to point, both in magnitude and direction. By convention, the direction of the electric field at a point is the direction of the force on a positive test charge placed at that point. An example of the electric field due to a positive point charge is given below.

 

Figure 9.3: Electric field lines of a positive charge