Angular position

The first is the angular position, conventionally denoted by $\theta$, as in Figure 5.1. This is the angle at a particular instant in time that the object makes with respect to some fixed reference axis. This angle may be measured in degrees, although in some instances it is more convenient to express it in a unit called radians. A radian is defined such that 2$\pi$ radians represents one complete revolution (360^o). The conversion is therefore 1 radian = (360/2$\pi$)^o. Since $\pi$ is approximately 3.14, this gives about 57^o per radian. Radians have special geometrical and physical significance, because for an object going in a circle, the distance traveled by the object (i.e. arc length) is precisely equal to the angular displacement in radians times the radius of the circle.

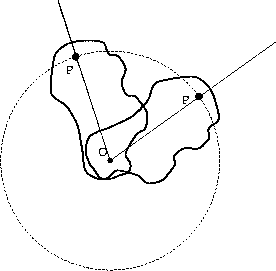
One of the reasons that the description of circular motion in terms of angular displacement is so useful is that it can be applied to the motion of extended, rigid objects rotating about a fixed axis. In particular, if an object, such as the one shown below, is rotating about an axis through the point, O, its motion is completely described by the angle through which any point in the object has rotated about that axis. This is true because every point in the object must rotate around the axis the precisely the same number of times per second, otherwise the object would break apart, or deform.

  

Figure 5.2: Rotation of an extended object about a fixed axis.