Potential Energy

The preceding considerations applied to any system, however complicated, for which a force or combination of forces is acting. Let us in this section confine ourselves to a certain type of force (called a ``conservative force''), for which some further simplifications are possible.

In particular, for a conservative force one can always find what is called a potential energy such that the work done by this force is given by

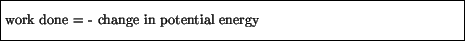
where the ``change'' in some quantity ``X'' is defined as

Note that only changes in potential energy have physical relevance.

If we now use the fact that the work done on an object equals the change in that object's kinetic energy, we then have

$\parbox{4.5in}{\vspace*{5pt} - change in potential energy = change in kinetic energy \vspace*{5pt}}$

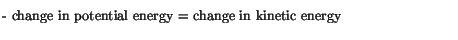
or, in other words,

$\parbox{4.5in}{\vspace*{5pt} change in kinetic energy + change in potential energy = 0 \vspace*{5pt}}$

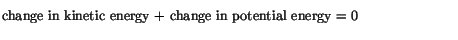
We now define for this situation the total energy of the system as

for which we can then say

    Two very fundamental concepts arise out of these considerations:

• The total energy of a system is conserved, or independent of time.
• The forms of energy (e. g., kinetic and potential) which comprise the total energy may be transformed into one another.

This latter point arises in situations where the kinetic and potential energy individually change in time, but always in such a way so that their total sum is constant. Thus, for example, one can gain kinetic energy at the expense of losing potential energy; in this case, potential energy is transformed into kinetic energy. One can thus never gain some form of energy without an accompanying loss of another form of energy, and vice-versa.

We now illustrate these concepts with three forms of potential energy.