Emission spectrum

Suppose an electron exists in a higher energy level (larger value of n). Systems generally like to be in as low an energy state as possible, and so the electron would fall into a lower energy state. However, this process by itself would involve a loss of energy, and so energy would not be conserved. To conserve energy, it was postulated that a particle called a photon carry away the excess energy in this transition, as pictured below.

 

Figure 12.4: Photon emission

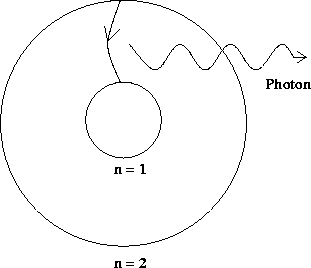Note that the energy of this photon is fixed, as it must be equal to the known difference in the energy levels of the electron transition. It would be natural to identify this photon with the light found when atoms emit light, and for this we need to know the frequency of the emitted light. Another hypothesis was put forward relating the energy of the photon to the frequency of the light wave:

where ``h'' is again Planck's constant.

Note that, for a given atom, there can be many types of transitions from higher to lower energies, and thus many different energies of emitted photons and, subsequently, many different frequencies of light waves. Some of these are illustrated below.

 

Figure 12.5: Possible transitions in the Bohr atom

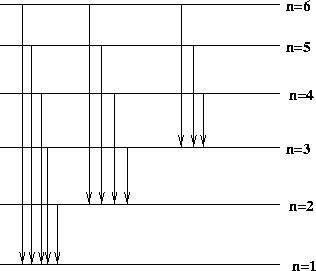Transitions ending up at the n = 2 level give rise to photons in the Balmer series, which is light in the visible part of the electromagnetic spectrum. Transitions to the n = 1 level give rise to the Lyman series, and to the n = 3 level give the Paschen series. Such series of distinct spectral lines are observed experimentally when a gas such as hydrogen is heated up - the added heat energy excites the electrons, which subsequently fall into lower energy levels, emitting photons of various energies and, thus, light of various frequencies. The observed frequencies correspond very well to what is predicted in the Bohr model.

This success of the Bohr model in explaining the emission spectra of simple atoms gave birth to an intense, and still on-going, investigation into what we now call quantum theory.