Refraction

Refraction is very easily understood within the wave model of light if one recalls that light slows down as it enters a more dense medium. If you imagine a long wave front approaching water from the air, as shown below.

 

Figure 10.13: Refraction of Waves

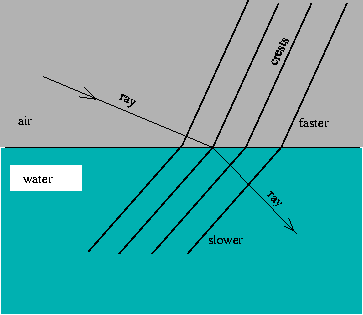The part of the wave front that is already in the water is going more slowly than the part that is still in the air. As a necessity, the wave front in the water ``turns'' inwards as shown. Think of a truck driving from pavement onto sand at a steep angle. The two front tires represent either end of a plane wave front (the truck's front axle). If the right tire hits the sand first it will slow down relative to the left tire, so that the axle (and hence entire truck) turns to the right. This is precisely how refraction of light works.

It is interesting to note that refraction of light is not definitive proof that light is a wave, since there is a way to explain it in terms of particle behaviour, as long as we are willing to make one additional postulate. Suppose that light is indeed made up of particles,and these particles slow down as they enter a more dense medium. Let us postulate that the particles of light follow paths that minimize the time it takes to arrive wherever they are going. This is called the principle of least action. We can understand the basic idea using the following heuristic description, due originally to Richard Feynman. Imagine that you are a life guard on a beach, and see someone drowning several meters off shore, as shown in the Figure below.

 

Figure 10.14: Principle of Least Action

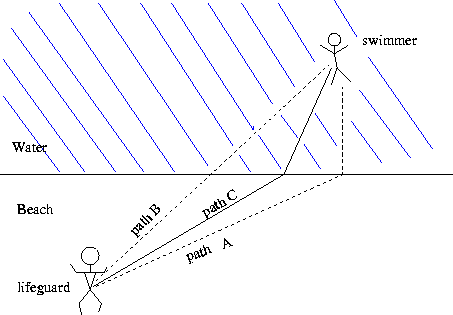Naturally you wish to get to the swimmer in the least amount of time possible. You know that you can run on the sand faster than you can swim, so you would like to spend as little time in the water as possible. One possibility is to run along the shore until you are directly opposite the drowning swimmer, and then swim from there, as in path A. The trouble is that this path is very long. An alternative approach would be to take the short path, (path A) which is the straight line between you and the swimmer. However, with this path you spend a fair bit of time swimming. It turns out that the correct path for optimizing the time it takes is the one that is a compromise between paths A and B, namely path C in the figure. Given the relative speeds on the sand and in the water, there is a specific angle through which you have to ``refract'' in order to have the greatest chance of saving the swimmer. If one applies this argument to light, one gets precisely the right quantitative predictions for the refraction of light. One must keep in mind that this behaviour is very natural for lifeguards, who know where they wish to go and why, but is, to say the least, a bit strange when applied to particles of light. So at this stage, it seems easier to just think of light as waves.