



Next: Newton's Third Law
Up: Force
Previous: Newton's First Law
If
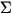
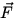
 0 (i.e. there is a net external force acting on an
object) then,
0 (i.e. there is a net external force acting on an
object) then,
Definition: Inertia is the tendancy of an object to resist any
attempt to
change its state of motion.
Mass is the force required per unit of acceleration produced and is a
measure of inertia. Mass is a scalar and has SI units of kilograms (kg).
Example: If a bowling ball and a golf ball are hit with a bat, the bowling
ball would be much harder to get moving since it has greater mass and thus
greater inertia.
Note:
-
 is inversely proportional to m . This means that, for the
same force, a smaller mass will have a larger acceleration.
is inversely proportional to m . This means that, for the
same force, a smaller mass will have a larger acceleration.
- Newton's second law is a vector equation which contains three scalar
equations (in three dimensions):
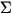 Fx = max ,
Fx = max ,
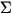 Fy = may ,
Fy = may ,
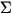 Fz = maz .
Fz = maz .
- The first law is a special case of the second law.
- The SI unit of force is the Newton (N). Definition:
1 Newton is the
force that produces an acceleration of 1 m/s 2 when acting on a 1 kg mass.
In the cgs system: 1 dyne = 1 g cm/ s 2= 10- 5N. In the British
engineering system: 1 pound (lb) = 4.448 N.
Definition: Weight ( 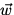 ) is the force exerted on an
object by
a gravitational field. From Newton's second law,
) is the force exerted on an
object by
a gravitational field. From Newton's second law,
Note:
- Weight is a vector with direction towards the earth's center, or
perpendicular to the earth's surface.
- The weight of an object is different on the earth and on the moon since
the strength of the gravitational field is different (
gearth
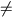 gmoon ).
gmoon ).
- The value of g varies with distance from the center of the earth (more
on this in chapter 7). As a consequence:
- Since the earth isn't a perfect sphere, the weight of an object
varies slightly from place to place on the earth's surface.
- The weight of an object varies slightly with altitude above the earth's surface.
- In comparison, mass is a scalar with a value independent of location.
Notice however that, in the approximation that g is constant, mass is
proportional to the magnitude of the weight and the two quantities can be used
interchangeably. This is called the equivalence principle.




Next: Newton's Third Law
Up: Force
Previous: Newton's First Law
www-admin@theory.uwinnipeg.ca
10/9/1997
![]()
![]()
![]()
![]()
![]() ) is the force exerted on an
object by
a gravitational field. From Newton's second law,
) is the force exerted on an
object by
a gravitational field. From Newton's second law,