Next: About this document ... Up: Solids and Fluids Previous: Fluids in Motion
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Solids and Fluids
Previous: Fluids in Motion

A steel railroad track is 1000 m long. When its temperature is
raised from -30 o to + 30 o thermal expansion
causes the length of the track to increase by .01%. What
compressive force per unit area would be required to keep
the track from expanding? (Hint: Calculate the force that would be
required to
compress it back to its original length. Young's modulus for steel
is
2 x 1011 N/m 2.
Solution:
|
| = |
Y | |
| = | 2 x 1011 N/m 2 x (1 x 10- 4)2 | ||
| = | 2 x 107 N/m 2. |
![]()
What is the approximate bulk modulus of the egg in our egg
experiment?
Solution:
We assume the egg to be a sphere of radius 5 cm, and that it is
compressed
by 2 mm in order to squeeze through the opening in the jar. If we
assume the jar to be completely evacuated, the
volume stress is simply the air pressure (1 Atm) and the volume
strain is:
|
| = |
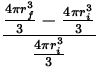
| |
| = | 0.115. |
| B | = |
- 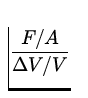
| |
| = |
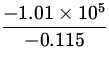
| ||
| = | 8.76 x 105 Pa. |
![]()
A boy tries to use a garden hose to supply air for a swim at the
bottom
of a 50m deep pool. What goes wrong?
Solution:
The pressure of air in his lungs and in the hose is at 1 atmosphere
(
1.01 x 105 Pa ),
whereas the pressure of the water pushing in on his lungs and on
the hose is:
| P | = |
P0 + | |
| = | (1.01 x 105) + (1.00 x 103)(9.8)(50) | ||
| = | 5.91 x 105 Pa. |

A car weighing
1.2 x 104 N rests on four tires. If the
gauge
pressure in each tire is 200 kPa, what it the area of each tire in
contact
with the road?
Solution:
Each tire must carry a weight of:
F = 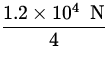 = 0.3 x 104 N.
= 0.3 x 104 N.
| P | = |
| |
|
| = |
| |
| = |
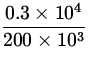
| ||
| = | 0.015 m 2. |
![]()
The same car as in the problem above sits on a hydraulic press as
shown
below. If the area of the cylinder holding the car up is 4 times
greater
than the area of the cylinder on the other side of the press, what
is the
force that must be applied to the other side of the hydraulic
press.
Solution:
|
P = | = |
| |
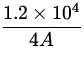
| = |
| |
|
| = | 0.3 x 104 N . |
![]()
An aluminum object has a mass of 27.0 kg and a density of
2.70 x 103
kg/m 3. The object is attached to a string and immersed in a
tank of
water. Determine the a) volume of the object b) the tension in the
string
when it is completely immersed.
Solution:
|
| = |
2.70 x 103 kg/m 3 = | |
|
| = |
| |
| = |
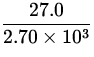 = 0.01 m 3. = 0.01 m 3.
|
|
| = | T + B - mg | |
|
| = | mg - B | |
| = |
mg - | ||
| = | (27.0)(9.8) - (1.00 x 103)(9.8)(0.01) | ||
| = | 166.6 N |
![]()
A garden hose of diameter 2 cm is used to fill a 20 liter bucket.
a) If it
takes 1 minute to fill the bucket, what is the speed at which water
enters
the hose? b) A practical joker pinches the open end of the hose
down to a
diameter of 5 mm, and sprays his neighbour with it. What is the
speed at
which water comes out of the hose?
Solution:
A1 = ![]() r 2 =
r 2 = ![]() (2 cm /2)2 =
(2 cm /2)2 = ![]() cm 2.
cm 2.
| Flow Rate | = |
A1v1 = 20.0 L/min = 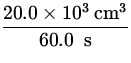
| |
|
| = |
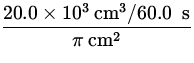
| |
| = | 106.1 cm/s. |
| v2 | = |
| |
| = |
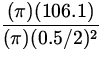
| ||
| = | 1698 cm/s. |
![]()
If a 30 m/s wind blows across a 175 m 2 flat roof of a house
a) what is the
pressure difference between the inside of the house and the outside
of the
house just above the roof? (Assume that the air pressure inside the
house is
atmospheric pressure.) b) What is the force on the roof due to the
pressure
difference?
Solution:
|
| = |
P out - P in = 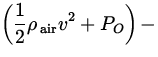 PO PO
| |
| = |
| ||
| = |
|
|
F = |

Water flows through the pipe shown below at a flow rate of
0.10 m 3 /s . The diameter at point 1 is 0.4 m. At point 2,
which is 3.0 m higher than point 1, the diameter is 0.20 m. If the
end at point 2 is open to the air, determine the gauge
pressure at point 2.
Solution:
First we use the fact that the flow rate must be the same at both
ends of the pipe to determine the velocities v1 and v2 at
points 1 and 2, respectively:
| A1v1 = A2v2 | = | 0.1 m 3/ s | |
|
| = |
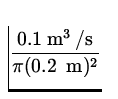
| |
| = | 0.8 m/s | ||
|
and | = |
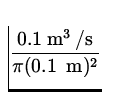
| |
| = | 3.2 m/s | (19) |
| P1 - P2 | = |
| |
| = |
| ||
| = | 43,800 N/m 2 | (20) |
www-admin@theory.uwinnipeg.ca