Angular velocity

In analogy with the concept of velocity for linear motion, the angular velocity for rotational motion can be defined. One first introduces the average angular velocity over a time by which the object moves from a point A on a circle to B:

The instantaneous angular velocity at a point A is then defined to be the average angular velocity between A and a point B as the point B approaches A:

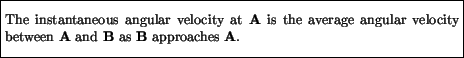
Angular velocity is measured in radians / second, although for motors in particular it is commonly expressed in rpm (revolutions per minute).

As an example, consider a car traveling at 30 m/s (approximately 110 km/hr). Given that tires have a radius of about half a meter, we can figure out the angular velocity of the tires, either in revolutions per second or radians per second. The circumference of the tires is 2$\pi$ times the radius. For a radius of half a meter, the circumference is $\pi$ meters. Therefore in order for the tires to go 30 m in one second they have to rotate 30/$\pi$ times every second, which is a rotation rate of about 9.55 revolutions per second. Since each revolution corresponds to an angular displacement of 2$\pi$ radians, this is the same as 9.55 x 2$\pi$ = 60 rads per second. So when you are traveling at 110 km/hr, your tires are rotating almost ten times per second. Conversely, if you know the rotation rate and radius of your tires, you can calculate the speed of the car, assuming that there is no slipping. This is precisely how the speedometer in the car works: it measures the rotation rate of your wheels and then converts this to km/hour by effectively multiplying by the circumference of the tires. You might notice that when you car is on ice and the tires spin, the speedometer registers a fairly high speed even though you are not moving. On the other hand, if your tires lock and you go into a skid, the speedometer drops to zero even though you may still be moving rather fast.