Acceleration

As we will see in the next section, acceleration is a very important concept in Newtonian physics. Just as the velocity involves a rate of change of position in time, the acceleration of an object describes the rate of change of velocity. Also just as with velocity, there are two types of acceleration. The first - the average acceleration - involves the change in instantaneous velocity over a given time interval:

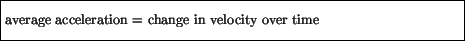
Note that, from now on, when we say ``velocity'', we will mean the instantaneous velocity. As well as a size, acceleration also involves a direction: for example, a car traveling on a road that runs due north accelerates from rest at a stop sign to a speed of 30 m/s in 10 seconds. That car experienced an average acceleration during that time of 30/10 m/s² or 3 m/s² with direction due north. In terms of km/hr, 30 m/s is:

$${30\space {\rm m}\over 1\space {\rm s}}$$ x $${1\space {\rm km}\over 1000\space {\rm m}}$$ x $${3600\space {\rm s}\over 1\space {\rm hr}}$$ = $${108\space {\rm km}\over 1\space {\rm hr}}$$

If the driver of the same car notices a radar trap and slows down to the speed limit of 60 km/hr, or about 17 m/s in, say 5 seconds, then the car undergoes an average acceleration due south of 17/5 m/s² = 3.4 m/s². In this case, the car is slowing down, or decelerating. Objects with a large acceleration change their velocity quickly over time.

We can also define the instantaneous acceleration at a point A as the limit of the average acceleration between A and a nearby point B as the interval between B and A becomes zero:

From now on, when we say ``acceleration'' we will mean the instantaneous acceleration.