




Next: Suggested Problems
Up: Rotation of Rigid Bodies
Previous: Rotational Kinetic Energy and
The general motion of a rigid body can be completely described by
the linear motion of its center of mass and its rotation about
the center of mass.
Newton's Second Law therefore has two parts:
Linear Motion
where
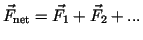 is
the net force on the object, M is the total mass,
is
the net force on the object, M is the total mass,
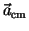 is th
acceleration of the center of mass of the object, and
is th
acceleration of the center of mass of the object, and
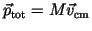 is its total linear momentum.
is its total linear momentum.
Rotational Motion
where
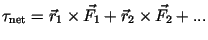 is the net torque on the object, I is its moment of
inertia about its center of mass, and
is the net torque on the object, I is its moment of
inertia about its center of mass, and 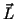 is its angular moment
about the center of mass.
is its angular moment
about the center of mass.
Note
-
When applying Newton's laws to solve for the motion of a system of
objects, one must apply the rotational version of the Second law to each
extended object in the system that is free to rotate.
-
In the absence of net external torque the total angular momentum of
any system of objects (about any axis) is conserved.





Next: Suggested Problems
Up: Rotation of Rigid Bodies
Previous: Rotational Kinetic Energy and
gabor@theory.uwinnipeg.ca
2001-01-05