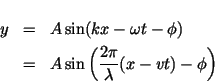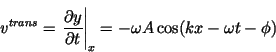Sinusoidal Waves:

  

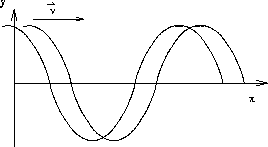
Figure 13: Moving sine wave

$$\begin{eqnarray*}y & = & A\sin(kx-\omega t-\phi ) \\ & = & A\sin\left(\frac{2\pi}{\lambda }(x-vt)-\phi\right) \end{eqnarray*}$$

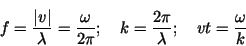$$f = \frac{\vert v\vert }{\lambda }=\frac{\omega }{2\pi }; \quad k = \frac{2\pi }{\lambda };\quad vt = \frac{\omega }{k}$$ (25)

Transverse velocity:

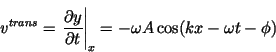$$v^{trans } = \left.\frac{\partial y}{\partial t}\right\vert _x = -\omega A \cos (kx-\omega t-\phi )$$ (26)

Wave equation:

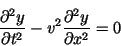$$\frac{\partial^2y}{\partial t^2} - v^2\frac{\partial^2y} {\partial x^2} = 0$$ (27)

Speed of transverse wave on string:

$$v = \sqrt{F/\mu }\qquad (\mbox{from\ Newton's\ 2nd\ Law})$$ (28)

Energy transmitted by sinusoidal wave:

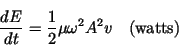$$\frac{dE}{dt} = \frac{1}{2}\mu\omega^2A^2v\quad \mbox {(watts)}$$ (29)