




Next: 3rd Law: The square
Up: Kepler's Laws:
Previous: 1st Law: Planets Orbit
Proof)
From the rotational analogue of Newton's 2nd law, namely
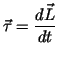 where
where
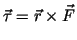 (torque) and
(torque) and
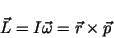 |
(8) |
we find that
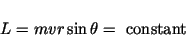 |
(9) |
which implies
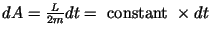 (see diagram above)
(see diagram above)
gabor@theory.uwinnipeg.ca
2001-01-05
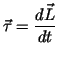 where
where