




Next: Kepler's Laws:
Up: GRAVITATION-Ch.14
Previous: Gravitational Potential Energy
We first consider the motion of planets and satellites in circular orbits.
Figure 5:
Circular Orbit
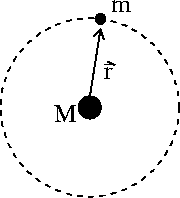 |
Total energy of a satellite of mass m in an orbit of radius r around a planet
of mass M is :
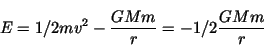 |
(7) |
where we have used the fact that the centripetal force is provided by
the force of gravity:
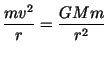 (
Fgrav = macentripetal)
(
Fgrav = macentripetal)
beginequation10pt]
gabor@theory.uwinnipeg.ca
2001-01-05

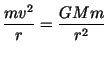 (
Fgrav = macentripetal)
(
Fgrav = macentripetal)